Question

1.диагонали ромба равны 12 см и 16 см. точка м, расположенной вне плоскостью ромба, удаленная от всех сторон на 8 см. найдите расстояние от точки м до плоскости ромба 2.радиус шара 9 см. определите объем шарового сектора, если дуга в осевом сечении сектора равен 90 градусов 3.через вершину конуса проведена плоскость под углом 45 градусов к плоскости основания. эта плоскость пересекает основание по хорде, расстояние до которой от вершины 6 см. найдите объем конуса, если длина радиуса - 5 см

Answer 1

Точка М равноудалена от сторон ромба, следовательно, проецируется в точку пересечения диагоналей ромба.

Расстояние от М до сторон равно длине отрезка МК, проведенного перпендикулярно  к стороне ромба. Проекции этого отрезка равна радиусу вписанной в ромб окружности, который, проведенный в точку касания К со стороной ромба перпендикулярен ей. 

Диаметр вписанной в ромб окружности равен высоте ромба. 

а) Для стороны ромба:

Сумма квадратов сторон параллелограмма равна сумме квадратов его диагоналей. Ромб - параллелограмм, все стороны которого равны. 

4 АВ²= 16²+12²=256+144=400

АВ²=100 ⇒ АВ=√100=10.

б) Для высоты ромба:

Площадь ромба равна половине произведения его диагоналей. 

S=12•16:2=96 см²

Площадь ромба равна произведению высоты на его сторону:

S=h•a;  96=h•10; h=9,6   ⇒ r=9,6:2=4,8 см

Из прямоугольного ∆ МОК  искомое расстояние 

МО=√(MK²-OK²)=√(64-23,04)=6,4 см

           * * * 

Формула объема шарового сектора V=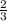$\frac{2}{3}$•πR²•h, где h - высота шарового сегмента с той же дугой в осевом сечении шара. 

На рисунке приложения это КН. 

∆ АОВ - прямоугольный, т.к. дуга АВ=90°

КО=АО•sin45°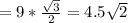$=9* \frac{ \sqrt{3} }{2} =4.5 \sqrt{2}$ см

KH=R-OK=9-4,5√2=2,636 см²

V=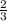$\frac{2}{3}$•π•81•2,636=142,346π см³

      * * * 

Пусть вершина конуса М, его высота МО, радиус ОА=5 см,  хорда АВ - основание сечения, его высота НМ=6 см является расстоянием от хорды до вершины конуса М. 

Угол, под которым плоскость пересекает плоскость основания конуса - угол между двумя проведенными  перпедикулярно к АВ  лучами МН и ОН. 

Тогда ∆ МОН - прямоугольный равнобедренный, НО=МО=МН•sin45°

$MO=6* \frac{ \sqrt{2} }{2} =3 \sqrt{2}$

V=S•h=πr²•h

V=π•25•3√2):3=π•25√2 см³

Answer 2

_____________________