1.180°-149°= 31°.
7. - (нет картинок, ничего не понятно, если добавишь позже, я отвечу)
8. -
9. -
10. АС= 37+10=47см, ВС= 47-5 =42 см; Р = АВ + АС + ВС = 37+42+47 = 126 см.
11. АВ = Р - ВС - АС = 60-26-15 = 19 см.
12.АС = 35+6 = 41 см, ВС = 41-9 = 32 см, Р = 35+32+41 см
13. ВС = 2ВЕ, т.к. АЕ медиана => ВС = 34,1×2 = 68,2 см.
14. ЕС =
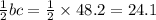
15. ЕС =
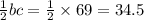
16.Рассмотрим ∆AMB, ∠ВАМ +∠АВМ = 180-120= 60°; Из точек А и В проведены биссектрисы => ∠А+В = 60 ×2 = 120°
17.∠В = 180-87-26 = 67°
18. Т.к. ∆АВС равнобедренный, ∠В=∠С => ∠А = 180 - (65+65) = 50°
19. Т.к. ∆АВС равнобедренный, ∠А=∠С; т.к. АD биссектриса, ∠DAC= 1/2 ∠A; Пусть ∠DAC - x, тогда ∠С= 2х, составим уравнение:
2х+х+105=180
3х=75
х=25 => ∠С=2×25 = 50°
20. ∠А= 180-51-53= 76°
Объяснение:
Объяснения написаны вместе с ответами :)
( Условие поняла, перевела с переводчика. но ответить могу только на русском, т.к. украинского не знаю)
--------------
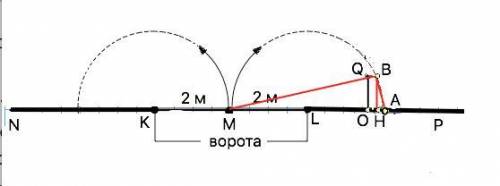
Автомобиль двигался по дороге параллельно забору NP и остановился около закрытых ворот КL так, как изображено на рисунке. Известно, что размах створки ворот LМ составляет 2 м, OQ=1 м. Укажите наименьшую из приведенных длин отрезка LO, при которой створка LM не заденет автомобиль, при условии полного открывания ворот. Считайте, что ворота перпендикулярны плоскости дороги и имеют прямоугольную форму. Толщиной створок пренебречь.
ответ: 1,8 м
Объяснение:
Если автомобиль остановится так, как на рисунке, при полном открывании ворот он будет задет ими задет, т.к. частично. расположен в описываемой створкой полуокружности. .
Решение. От Q вправо проведем прямую до пересечения с линией полуокружности в т.В. От В проведем отрезок ВА ( А - на линии забора).
Треугольник МВА - прямоугольный ( опирается на диаметр МА. Перпендикуляр ВН - высота этого треугольника.
Искомое расстояние - LH.
ВН=QO=1 м по построению. Высота прямоугольного треугольника - среднее пропорциональное отрезков, на которые она делит гипотенузу ( здесь - диаметр МА). =>
ВН²=МН•НА
ML=LA=2 м
Примем LH=x. Тогда МН=2+x, АН= 2-x
(2+х)•(2-х)=1²
4-х²=1 ⇒ х=√3=1,732 ≈1,8 м
Расстояние LO не должно быть менее 1,8 м
Если в равнобедренной трапеции провести высоты ВН и СК, то получим НВСК - прямоугольник (ВС║КН, так как основания трапеции параллельны, ВН║СК как перпендикуляры к одной прямой), тогда
ВС = КН и ВН = СК.
ΔАВН = ΔDCK по гипотенузе и катету (АВ = CD, так как трапеция равнобедренная, ВН = СК), тогда
АН = DK = (AD - KH)/2 = (AD - BC)/2.
Площадь трапеции:
Sabcd = (AD + BC)/2 · BH
Воспользуемся этими выводами для решения задач:
а) AH = DK = (17 - 11)/2 = 3 см
ΔАВН прямоугольный с гипотенузой, равной 5 см и катетом 3 см, значит он египетский и
ВН = 4 см.
Sabcd = (17 + 11)/2 · 4 = 28/2 · 4 = 14 · 4 = 56 см²
б) AH = DK = (8 - 2)/2 = 3 см
ΔABH: ∠AHB = 90°, ∠BAH = 60°, ⇒ ∠ABH = 30°.
AB = 2AH = 6 см по свойству катета, лежащего напротив угла в 30°,
по теореме Пифагора:
BH = √(AB² - AH²) = √(36 - 9) = √27 = 3√3 см
Sabcd = (8 + 2)/2 · 3√3 = 15√3 см²