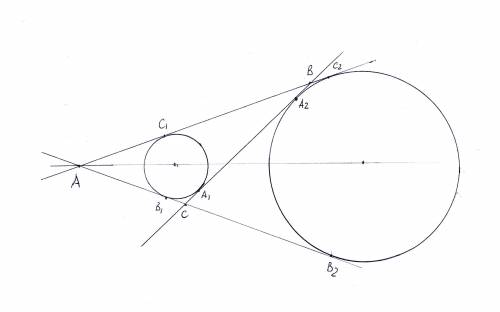
Все дело в том, что этот отрезок равен отрезку внешней касательной между точками касания. См. рисунок.
Ясно, что В1В2 = С1С2 - это симметричные относительно линии центров отрезки. Далее,
В1В2 - СВ1 = СВ2 = СА2 = СА1 + А1А2;
С1С2 - С2В = ВС1 = ВА1 = ВА2 + А1А2;
Поэтому
В1В2 = А1А2 + СА1 + СВ1 = А1А2 + 2*СА1;
C1C2 = А1А2 + ВА2 + ВС2 = А1А2 + 2*ВА2;
Отсюда
СА1 = ВА2 и ВС = С1С2 = В1В2;
(Я очень советую во всем этом разобраться! Это только кажется, что - просто)
Дальнейшее решение я на рисунке не изображаю - надо провести радиусы О1С1 и О2С2, и из точки С1 - прямую II О1О2 (это центры окружностей, О1 - ближе к А). Получается прямоугольный треугольник, в котором гипотенуза равна О1О2 - заданному расстоянию между центрами, один из катетов R - r, а второй - С1С2=ВС, которую надо найти.
О1О2^2 = (R - r)^2 + BC^2;
Я не буду доделывать - у вас там ошибка, расстояние не может быть равно Rr, скорее всего там корень - чтобы РАЗМЕРНОСТЬ была правильной. В любом случае
ВС^2 = d^2 - (R - r)^2; (d - заданнное расстояние между центрами)
центр описанной окружности равноудален от вершин треугольника => радиус можно найти из треугольника OBC, кот. будет РАВНОБЕДРЕННЫМ с основанием 18 и равными боковыми сторонами R, высота этого равнобедренного треугольника, проведенная из точки O (обозначим OH) будет и биссектрисой и медианой, по т.Пифагора из полученного прямоугольного треугольника
OB^2 = R^2 = OH^2 + (18/2)^2
все углы равностороннего треугольника =60 градусов
угол OBH = 60/2 = 30
OH---катет против угла в 30 градусов равен половине гипотенузы = R/2
R^2 = (R/2)^2 + 9*9
R^2 = R^2/4 + 9*9
4R^2 = R^2 + 9*9*4
4R^2 - R^2 = 9*9*4
3R^2 = 9*9*4
R^2 = 9*3*4
R = 3*2*корень(3) = 6*корень(3)
В правильной треугольной пирамиде двугранный угол при основании равен 60°. Отрезок, соединяющий основание высоты пирамиды с серединой апофемы, равен 3. Найдите площадь полной поверхности пирамиды.
* * *
Решение.
Двугранный угол измеряется величиной линейного угла между двумя лучами, проведенными перпендикулярно к одной точке ребра двугранного угла.
Боковая грань правильной пирамиды - равнобедренный треугольник. Апофема МН и высота СН основания перпендикулярны ребру АВ в его середине Н. АН=ВН.
Угол МНС - линейный угол двугранного угла при основании пирамиды.
Вершина правильной пирамиды проецируется в центр основания - точку пересечения его медиан ( высот, биссектрис).
Высота пирамиды МО - перпендикулярна плоскости основания,⇒
МО⊥СН.
∆ МОН - прямоугольный, КО - его медиана.
По свойству медианы прямоугольного треугольника МК=КН=КО=3, ⇒ МН=2•3=6
По условию ∠КНО=60°.
В ∆ КОН стороны КО=НК ⇒ НО=КО=3
СН медиана и высота основания АВС,
Медианы треугольника точкой их пересечения делятся в отношении 2:1, считая от вершины.
СН=3•ОН=9.
S ∆ ABC=CH•AB:2=0•6√3:2=27√3
S бок=3•МН•AB:2=3•6•6√3:2=54√3
Sполн=27√3+54√3=81√3 (ед. площади)