В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой. Доказательство.Обратимся к рисунку, на котором АВС — равнобедренный треугольник с основанием ВС, АD — его биссектриса.Из равенства треугольников АВD и АСD (по 2 признаку равенства треугольников:AD-общая;углы 1 и 2 равны т.к. AD-биссектриса;AB=AC,т.к. треугольник равнобедренный) следует, что ВD = DC и 3 = 4. Равенство ВD = DC означает, что точка D — середина стороны ВС и поэтому АD — медиана треугольника АВС. Так как углы 3 и 4 смежные и равны друг другу, то они прямые. Следовательно, отрезок АО является также высотой треугольника АВС. Теорема доказана. В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой Если в треугольнике два угла равны, то он равнобедренный. Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.
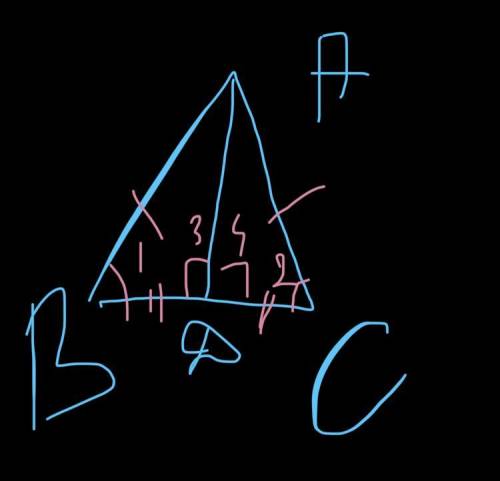
В трапеции биссектриса отсекает от противолежащего основания (или его продолжения) отрезок, равный прилежащей боковой стороне (свойство трапеции). ВД - биссектриса угла Д, значит ВС=СД=10 см.
Опустим высоту СК⊥АД.
КД=АД-АК=АД-ВС=18-10=8 см.
В треугольнике СДК СК²=СД²-КД²=10²-8²=36,
СК=6 см.
S=h(a+b)/2=СК(АД+ВС)/2=6(18+10)/2=84 см² - это ответ.