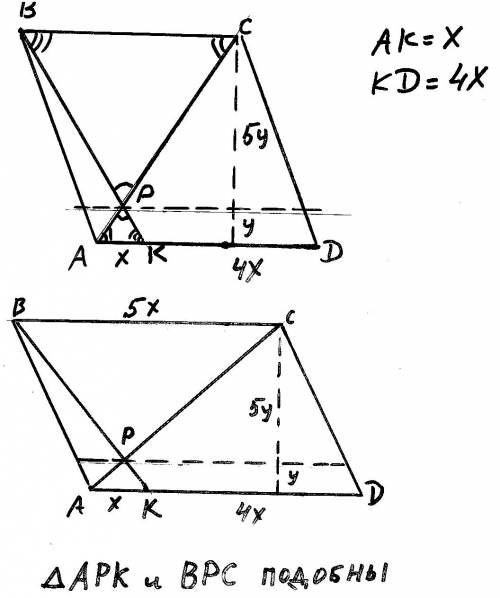
Треугольники АРК и ВРС подобны (смотри рисунок) по трём углам(вертикальный и накрест лежащие). Пусть АК=Х, тогда КД=4Х, а ВС=АД=Х+4Х=5Х. ВС/АК=5Х/Х=5. Это и есть коэффициент подобия. Следовательно если высота треугольника АРК равна У, то высота треугольника ВРС равна 5У. Найдём площади. Sарк=1/2*Х*У=1. Тогда Х*У=2. Площадь параллелограмма равна Sавсд=АД*Н=5Х*6У=30Х*У. Подставляем значение Х*У=2, получим Sавсд=30*2=60. Эта задача интересна тем, что при заданном условии можно построить множество параллелораммов с площадью=60(на рисунке в качестве примера представлено два). Если интересно могу написать как это делается.
Если ВНИМАТЕЛЬНО посмотреть на треугольник SKB (постройте его! - это сечение пирамиды по боковому ребру BS и точке К, в нем лежит высота пирамиды), то мы увидим, что нам известно про это треугольник почти всё. Пусть О - проекция S на основание. По теореме синусов (!) находим ОВ = АС/(2*sin(60)) = 3 - это радиус описанной вокруг основания окружности.
Рассмотрим треугольник SKB ещё внимательнее :)) Проекция точки М на ВК отстоит от точки О на 1/4 ОВ.
Очень легко увидеть, что при этом она попадает точно в середину ВК. Я даже не стану тут вычислять - проверьте сами, уж сложить 1/4 от 2/3 с 1/3 и получить 1/2 сможет даже экономист :))) не каждый, конечно, но говорят, что среди академиков такие встречаются :)))
Это означает, что треугольник КМВ - равнобедренный, и угол МКВ = Ф (который и надо найти) равен углу SBO, который найти проще, чем набрать это текст.
ответ cos(Ф) = ОВ/SB = 3/5
32=4а
а=8см
Sкв=а×аSkв=64см2
Sпаралелограма=Sкв=64
Sпарал=а×ha
64=a×4
a=16см