Объяснение:1. Измерение отрезков
Две геометрические фигуры (отрезки, углы,
треугольники и др.) считаются равными, если их
можно наложить друг на друга так, чтобы они совпали.
Отрезки равны, если равны их длины.
Если точка лежит на отрезке , то A B C
+ = .
1. На прямой выбраны три точки , и , причём = 3, = 5. Чему может быть равно ?
(Есть разные возможности.)
B Если точка находится между точками и
A B C
3 5
, то это расстояние равно 3+5 = 8. Но возможен и
другой случай, когда находится вне отрезка .
Нарисовав картинку, убеждаемся, что в этом случае
B A C расстояние равно 5 − 3 = 2. C
3 2
2. На прямой выбраны четыре точки , , ,
, причём = 1, = 2, = 4. Чему может
быть равно ? Укажите все возможности.
B Сначала посмотрим, чему может быть равно
расстояние между точками и . Как и в предыдущей задаче, тут есть две возможности (точка
внутри или вне) | и получается либо 3, либо
1. Теперь мы получаем две задачи: в одной из них
= 3 и = 4, в другой | = 1, = 4.
Каждая имеет по два ответа, так что всего ответов
получается четыре: 4+3, 4−3, 4+1 и 4−1. ответ:
расстояние может равняться 1, 3, 5 или 7. C
3. На деревянной линейке отмечены три деле- 0 7 11
ния: 0, 7 и 11 сантиметров. Как отложить с её отрезок в (а) 8 см; (б) 5 см?
B Используя деления 7 и 11, легко отложить 4
сантиметра. Сделав это дважды, получим отрезок
в 8 сантиметров. Отложить 5 сантиметров немного
сложнее: умея откладывать 8 и 7, можно отложить
1 сантиметр. Сделав это 5 раз, получаем
Профессорская задачка :)
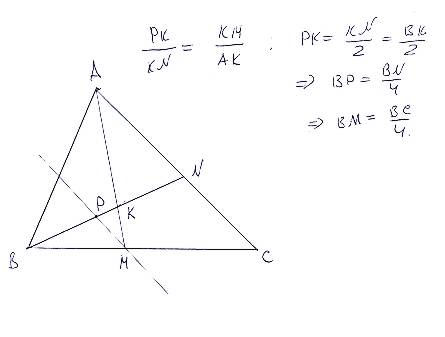
1. Вс задача. В произвольном треугольнике две прямые, выходящие из разных вершин, делятся в точке пересечения в отношении 2:1 и 1:1. Нужно найти, в каком отношении они делят стороны. На самом деле, для заданной задачи достаточно найти, в каком отношении делится сторона, к которой проведена та прямая, которая длится в отношении 2:1. На первом рисунке - простое решение этой задачи. (Не надо путать обозначения тут и при решении основной задачи).
Задано ВК/KN = 1; AK/KM = 2; надо найти BM/BC.
Проводится PM II AC, треугольники PKM и AKN подобны, и PK/KN = KM/AK = 1/2; но КN = BN/2, то есть PN = BN/4; тогда и BP = BN/4; а отсюда BM = BC/4;
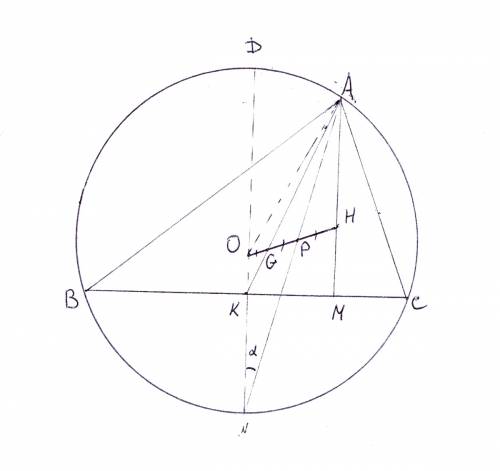
2. Собственно решение. Я изменил обозначение точки пересечения медиан трегольника АВС на букву G. O - центр описанной окружности, Н - ортоцентр. Точка Р пересечения биссектрисы угла А и GН делит GН пополам.
Поскольку АР - биссектриса угла А, то её точка пересечения с окружностью N делит дугу ВС пополам, то есть совпадает с точкой пересечения перпендикуляра к ВС из центра О.
Легко увидеть, что угол DNA между биссектрисой и этим диаметром, обозначенный как α, равен (угол АСВ - угол АВС)/2 (проще всего это понять, если провести через А хорду АА1 II ВС, тогда дуга ВА1 = дуга АС, и угол А1NA = угол А1СА, а DN биссектриса угла A1NA), то есть α = 15°;
Теперь самое главное. Точки O, G и Н лежат на прямой Эйлера, и OG = GH/2; Отсюда следует, что OG = GP = PH; кроме того, точка G делит АК в отношении AG/GK = 2 (ну, это же медиана тр-ка АВС...)
Согласно вс задаче из треугольника AON получается OK = ON/4; то есть расстояние от О до хорды ВС равно четверти радиуса окружности. Отсюда легко найти радиус R описанной окружности. R^2 = 1^2 + (R/4)^2; R = 4/√15;
Для того, чтобы найти площадь, нужно найти АМ. Центральный угол DOA равен 2α = 30°; и равен углу ОАМ, откуда сразу видно, что АМ = ОК + АО*cos(2α) = R*(1/4 + cos(2α)) = R(1/4 + √3/2);
S = ВС*АМ/2 = (4/√15)*(1 + 2√3)/8 = (1 + 2√3)/(2√15);
Я, конечно, мог и ошибиться в арифметике, так что проверяйте, но смысл решения понятен :)