A1. Две прямые на плоскости называются параллельными, если они:
4) не пересекаются
А2. Один из признаков параллельности двух прямых гласит:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А3. Выберите утверждение, являющееся аксиомой параллельных прямых:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
А4. Если две параллельные прямые пересечены секущей, то:
Соответственные углы равны
А5. Если прямая перпендикулярна одной из двух параллельных прямых, то:
Она перпендикулярна и другой
А6. Всякая теорема состоит из нескольких частей:
Условия и заключения
А7. При пересечении двух прямых секущей образуются углы, имеющие специальные названия:
Накрест лежащие, соответственные, односторонние
А8. Аксиома – это:
Положение геометрии, не требующее доказательства
А9. Выберите утверждение, которое является признаком параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А10. Если прямая не пересекает одну из двух параллельных прямых, то:
Другую прямую она тоже не пересекает
или
С другой прямой она совпадает
Объяснение:
1. <ABM=<BAC, <CBF=<ACB как накрест лежащие. Пусть x - 1 часть. Значит <ABM=3х, <ABC=5x, <CBF=2x. Их сумма равна 180гр. Значит 3x+5+2x=180 x=18.
<BAC=3*18=54, <ABC=5*18=90, <ACB=2*18=36
2.
ответ будет 50гр, но я решил через сумму четырехугольника.
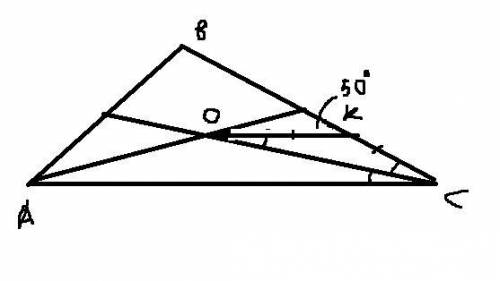
3. Рассмотрим тр-к OKC. В нём OK=KC по условию, значит он равнобедренный и <COK=<OCK. Но при этом он же будет равен <ACO т.к. CO - биссектриса. Отрезки OK и AC будут параллельны, т.к. в них накрест лежащие углы <COK и <ACO равны. (Теорема если при пересечении двух прямых секущей ( в данном случае биссектрисой CO) накрест лежащие углы оказываются равны, то значит, эти прямые параллельны.) Из этого следует, что cоответственные углы <BKO=<ACB=50гр при пересечении секущей BC. Тогда находим <COK=<OCK=1/2*<ACB=25гр
(-1;2)
АМ= ((-3+1)^2+(1-2)^2)^1/2=5^(1/2)