№1:  . №2:
. №2: 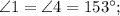
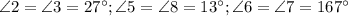 .
.
№1.
Пусть  , тогда
, тогда  - секущая.
- секущая.
Теорема: "При пересечении двух параллельных прямых секущей, сумма односторонних углов равна  .
.
 , по условию.
, по условию.
 и
и  - односторонние углы
- односторонние углы 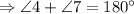
№2.
Обозначим данные прямые буквами 
Пусть  - секущая прямых
- секущая прямых  и
и 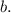
Теорема: "При пересечении двух параллельных прямых секущей, накрест лежащие углы равны".
 и
и 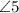 - накрест лежащие при пересечении
- накрест лежащие при пересечении  и
и  секущей
секущей  , однако
, однако 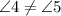 .
.

 и
и  - не параллельны.
- не параллельны.
============================================================
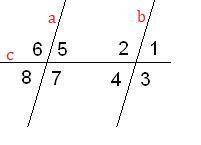
Свойство: "Вертикальные углы равны".
Свойство: "Сумма смежных углов равна  ".
".
Рассмотрим углы, образовавшиеся при пересечении прямых  и
и 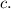
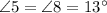 , по свойству вертикальных углов.
, по свойству вертикальных углов.
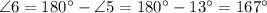 , по свойству смежных углов.
, по свойству смежных углов.
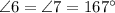 , по свойству вертикальных углов.
, по свойству вертикальных углов.
===========================================================
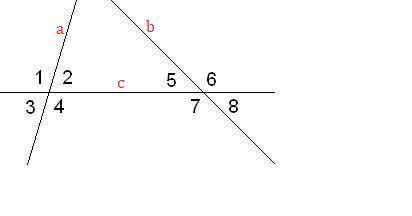
Рассмотрим углы, образовавшиеся при пересечении прямых  и
и  .
.
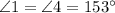 , по свойству вертикальных углов.
, по свойству вертикальных углов.
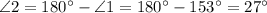 , по свойству смежных углов.
, по свойству смежных углов.
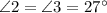 , по свойству вертикальных углов.
, по свойству вертикальных углов.
1. Соединим точки С и D с центром. Тогда треугольники AOD и ВОС равнобедренные (OA = OB = OC = OD как радиусы), ⇒
∠1 = ∠2 и ∠3 = ∠4.
∠2 = ∠3 как накрест лежащие при пересечении параллельных прямых AD и ВС секущей АВ. Но тогда в этих треугольниках равны и углы при вершине О. Значит треугольники AOD и ВОС равны по двум сторонам и углу между ними, ⇒
AD = BC.
2. Точки, находящиеся на данном расстоянии от данной прямой а, будут расположены на прямой, параллельной прямой а (красные прямые). В зависимости от расположения прямых задача может иметь одно решение (1), два решения (2) и не иметь решения (3).
168 : 2 = 84°