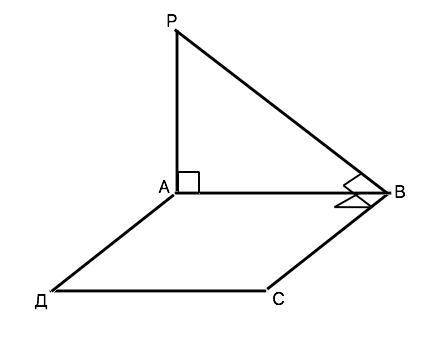
РА - перпендикуляр к площади параллелограмма АВСД. Укажите вид параллелограмма, если РВ перпендикулярен ВС. а) ромб, б) прямоугольник; в) квадрат.
Объяснение: РВ - наклонная. АВ - её проекция на плоскость АВСД. По т. о 3-х перпендикулярах если наклонная (РВ) перпендикулярна прямой (ВС) на плоскости, то её проекция на ту же плоскость перпендикулярна данной прямой. Следовательно, АВ⊥ВС, и угол АВС - прямой. Противоположные углы параллелограмма равны. ⇒ ∠Д=∠В=90°, поэтому из суммы углов четырехугольника ∠А+∠С=360°-2•90°=180°, и каждый из них равен 180°:2=90°.
Углы четырехугольника АВСД прямые. ⇒ АВСД - прямоугольник. Он может быть и квадратом. если его стороны будут равны.
ответ: Б), В).
Объяснение:
А) Неверно.
OD - высота и медиана равнобедренного треугольника MON, ОС - высота и медиана равнобедренного треугольника МОК.
Если бы отрезок СО был равен DO, то ΔODM был бы равен ΔОСМ по катету и общей гипотенузе ОМ. Но тогда были бы равны половины данных хорд, а по условию хорды не равны.
Б) Верно.
ΔMON равнобедренный (MO = NO как радиусы), OD - его высота, значит и медиана, следовательно OD - серединный перпендикуляр к MN.
В) Верно.
∠NMK = 90° по условию, этот угол вписанный, значит он опирается на полуокружность, т.е. NK - диаметр. Так как ОМ - радиус, то
NK = 2OM.
Г) Неверно.
МО - медиана треугольника NMK. Если бы отрезок МО был биссектрисой, то треугольник NMK был бы равнобедренным, а по условию MK ≠ MN.