1. 4 см.
2. 84 см.
3. 2√26 см.
Объяснение:
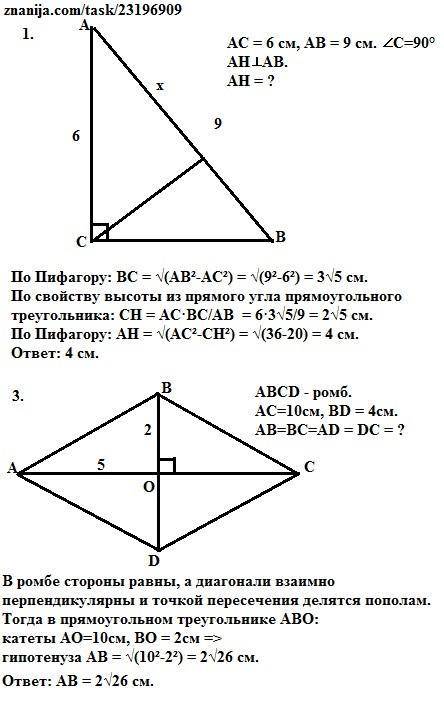
1. По Пифагору: ВС = √(АВ²-АС²) = √(9²-6²) = 3√5 см.
По свойству высоты из прямого угла прямоугольного треугольника:
СН = АС·ВС/АВ = 6·3√5/9 = 2√5 см.
По Пифагору: АН = √(АС²-СН²) = √(36-20) = 4 см.
ответ: 4 см.
2. По Пифагору второй катет равен √(37²-35²) = √(2·72) = 12см. Тогда периметр треугольника (сумма его трех сторон) равен:
37+35+12 = 84см.
ответ: 84см.
3. В ромбе стороны равны, а диагонали взаимно перпендикулярны и точкой пересечения делятся пополам.
Тогда в прямоугольном треугольнике АВО:
катеты АО=10см, ВО = 2см =>
гипотенуза АВ = √(10²-2²) = 2√26 см.
ответ: 2√26 см.
b : a = 3 : 2,5
Свойство пропорции - произведение крайних членов равно произведению средних
2,5b = 3a
b = 3a/2,5
b= 1,2a
b/2 = 0,6a
По теореме Пифагора
h² + (b/2)² = a²
8² + (0,6a)² = a²
64 + 0,36a² = a²
a² - 0,36a² = 64
0,64a² = 64
a² = 64/0,64
a² = 100
a = 10 (см)
b= 1,2 * 10 = 12 (см)
b 2a -b
r = √()
2 2a+b
где r - радиус вписанной окружности, а - боковая сторона равнобедренного треугольника, b - основание треугольника
12 2 * 10 - 12
r = * √( ) = 6 * √(8 / 32) = 6 * √(1/4) = 6 * 1/2 = 3 (cм)
2 2 * 10 + 12