Медианы треугольника пересекаются в одной точке. Эта точка делит каждую медиану в отношении 2:1 (считая от вершины).
Медианы в правильном треугольнике равны.
R =10см - 2 части - отрезок от точки пересечения медиан до вершины
Вся медиана - 15см
ответ: 15 см
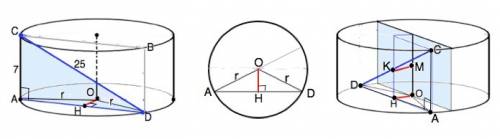
Прямые, содержащие СD и ось цилиндра, не параллельны, не пересекаются, - они скрещивающиеся.
Расстояние между скрещивающимися прямыми равно расстоянию между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
Расстояние от любой точки прямой до плоскости которой эта прямая параллельна, одинаково и равно длине отрезка, проведенного перпендикулярно от прямой к плоскости.
Образующая СА - высота цилиндра, АD - проекция СD на его основании.
CA перпендикулярна плоскости основания, ⇒
СА⊥AD
∆ САD- прямоугольный. По т.Пифагора АD=24.
Соединим А и D с центром О основания.
Треугольник АОD равнобедренный ( две его стороны - радиусы), ОН - его высота и искомое расстояние.
ОА=ОD=r
r=d/2=13
АН=AD:2=12
По т.Пифагора ОН=5 см. - это ответ.
———————
Можно провести плоскость через диаметр цилиндра параллельно СD, где НО=КМ (см. рисунок).
Треугольник OMC прямоугольный (прямой угол M) с гипотенузой |OC| = 6*корень(3)/2 = 3*корень(3) и уже найденным катетом |OM|. Второй катет по Пифагору корень(3*3*3 - 3*3) = 3*корень(2).
Проекцию OM на плоскость треугольника ABC (обозначим x) можно найти по подобию: x/|OM| = |OM|/|OC| или x = 3*3/(3*корень(3)) = корень(3)
Площадь проекции всего треугольника составит половина произведения x (ее высоты) на основание AB или 0.5*6*корень(3) = 3*корень(3).
Ну вроде бы так, если не запутался.