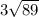
Объяснение:
Объём пирамиды:
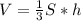, где S - площадь основания, h - высота пирамиды.
Значит 
У правильной четырёхугольной пирамиды основанием выступает квадрат. Если сторону квадрата обозначить как а, то S=a² ⇒ а=√S.
Боковое ребро пирамиды l, её высота h и полудиагональ основания образуют прямоугольный треугольник, в котором искомое ребро - гипотенуза, а высота и полудиагональ - катеты.
Диагональ квадрата равна √(2а²)=а*√2,
тогда половина диагонали равна а/√2, а так как а=√S,
то половина диагонали равна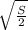 
Тогда, по теореме Пифагора:
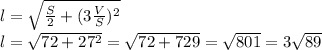
АВ=АС/sin60=10·2/√3=20√3/3 см.
Катет ВС лежит напротив угла в 30°, значит ВС=АВ/2=10√3/3 см.
Площадь S=АС·ВС/2=10·10·√3/6=50√3/3 см.