Дано:
O - центр окружности
AB = 4 см
CM - AM = 4 см
Найти: r (радиус окружности)
CM = CO + OM = r + OM
AM = OA - OM = r - OM
CM - AM = 4
r + OM - r + OM = 4
2×OM = 4
OM = 2 ⇒ CM = r + 2, AM = r - 2
Рассмотрим ΔMBA - прямоугольный
По теореме Пифагора:
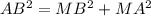
Рассмотрим ΔABC - прямоугольный, так как ∠ABC = 90° (опирается на диаметр)
По теореме Пифагора:
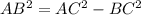
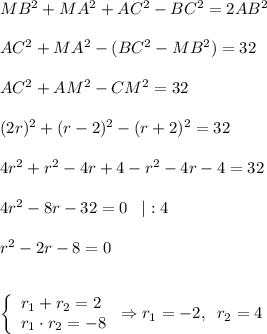
r₁ = -2 не подходит, так как радиус не может быть отрицательным, следовательно r = 4
ответ: 4 см
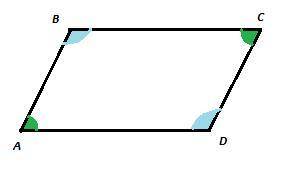
Противоположные углы параллелограмма равны между собой, соседние углы параллелограмма в сумме равны 180°.
∠A=∠C; ∠B=∠D; ∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°
1) Острый угол параллелограмма равен 46°
∠A = 46°; ∠B = ∠D = 180° - 46° = 134°
∠A = ∠C = 46°; ∠B = ∠D = 134°
2) Так как сумма двух углов 186° больше 180°, значит, это сумма двух тупых углов параллелограмма.
∠B + ∠D = 186°; ∠B = ∠D = 186° : 2 = 93°
∠A = ∠C = 180° - 93° = 87°
3) Тупой угол параллелограмма на 56° больше острого угла.
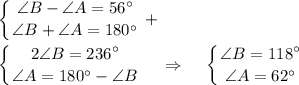
∠A = ∠C = 62°; ∠B = ∠D = 118°
4) Острый угол параллелограмма в 3 раза меньше тупого угла.
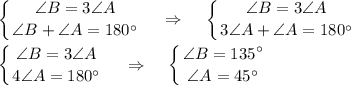
∠A = ∠C = 45°; ∠B = ∠D = 135°
5) Острый угол относится к тупому углу как 5:7
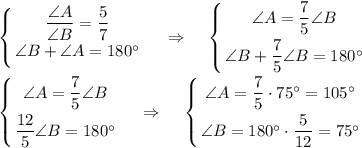
∠A = ∠C = 75°; ∠B = ∠D = 105°
r=4 см
Объяснение:
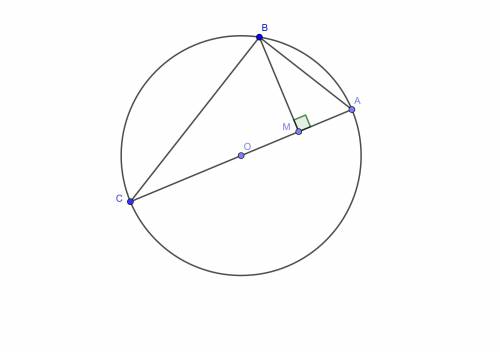
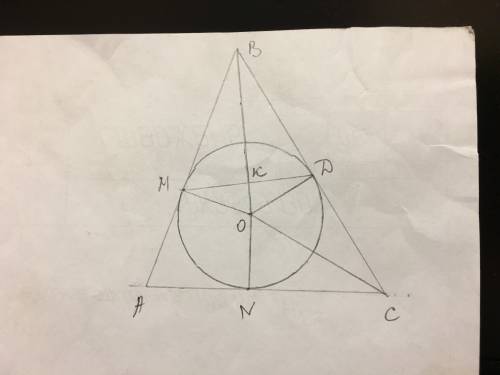
Дано: АС - диаметр окружности, точка В лежит на окружности, ВМ⊥АС, СМ=АМ+4.
Найти: r.
Рисунок к задаче смотри в прикрепленном файле.
Пусть АМ=х, тогда МС=х+4.
ΔАВМ прямоугольный, т.к. ВМ⊥АС (по условию).
По теореме Пифагора найдем ВМ.
Проведем отрезок ВС. ΔАВС прямоугольный, т.к. вписан в окружность и одна его сторона является диаметром окружности.
ВМ - высота, проведенная из вершины прямого угла к гипотенузе - вычисляется как корень квадратный из произведения длин отрезков, на которые высота поделила гипотенузу.
Мы получили два разных выражения, при которых можно найти длину отрезка ВМ. Поскольку результат у них будет одинаковый, приравняем их.
По теореме Виета x₁=-4, х₂=2.
х=-4 - посторонний корень (т.к. длина отрицательной быть не может).
АМ=2, МС=2+4=6.
АС=АМ+МС=2+6=8
ответ: r=4 см.