ответ: a) 62°; б) 118°
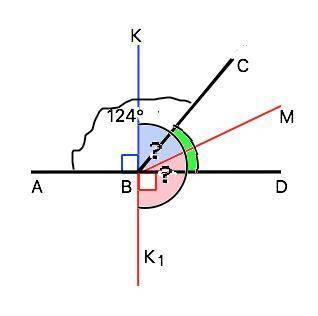
Объяснение: Вопрос явно неполный - не указан второй из смежных углов. Правильно: Углы ABC и BCD – смежные, причем угол ABC равен 124 градуса. Найдите угол между перпендикуляром, проведенным из точки B к прямой AD и биссектрисой угла CBD.
* * *
Сумма смежных углов 180°, поэтому ∠СВD=180°- ∠ABC=180°-124°=56°.
Обозначим биссектрису угла СВD как ВМ. Биссектриса угла делит его пополам, поэтому ∠СВМ=∠DBM=56°:2=28°
У задачи 2 варианта решения.
а) Перпендикуляр ВК к прямой AD лежит в той же полуплоскости, что луч ВС. Тогда искомый угол КВМ=∠КВD-∠MBD=90°-28°=62°
б) Перпендикуляр ВК1 лежит во второй полуплоскости. Тогда искомый угол К1ВМ=∠K1BD+∠DBM=90°+28°=118°
ABCD - трапеция
BK и CN - высоты из В и С на AD.
AD = 18 cм.
AB = CD
L A = L D = 60 град.
Пусть AK = ND = x
AB = AK / cos 60 = 2AK = 2x
CD = ND / cos 60 = 2ND = 2x
KN = BC
AD = AK + KN + ND = 2x + KN = 2x + BC = 18
AD + BC = AB + CD
(2x + BC) + BC = 2x + 2x
2BC = 2x
{BC = x =
{2x + BC = 18
2x + x = 18
3x = 18
x = 6 =>
AB = 2x = 2*6 = 12 см
AK = x = 6 =>
BK^2 = AB^2 - AK^2 = 12^2 - 6^2 = 108 = (10,4)^2
BK = 10,4 см - высота трапеции, она де диаметр вписанной окружности.
S = пD^2 /4 = 3,14 * 10,4^2 / 4 = 84,78 см^2
ты проверь на всякий случай ( я часто ошибаюсь