Проекции катетов на гипотенузу прямоугольного треугольника - это отрезки гипотенузы, на которые ее делит высота, т.к. высота - перпендикуляр к прямой ( гипотенузе), а катеты – наклонные из вершины прямого угла.
Катет - среднее пропорциональное между гипотенузой и его проекцией на неё .
В треугольнике на рисунке приложения
Катет Вс=30 см, а ВН=18 - его проекция на гипотенузу.
BC²=АВ•НВ
900=АВ•18
АВ=900:18=50 см
Высота, проведенная к гипотенузе, делит прямоугольный треугольник на подобные. Из подобия следует отношение:
АН:АС=АС:АВ
АН=50-18=32
32:АС=АС:50 ⇒ АС²=32•50
АС=√1600=40 см
Если обратить внимание на отношение катета и гипотенузы 3:5 в ∆ ВСН, увидим, что этот треугольник - египетский. Отсюда следует АВ=50 см, (т.к. меньший катет=30). а АС=40 см. Получим длины сторон треугольника, отношение которых 3:4:5.
Объяснение:
Відповідь:
A1C и DB равен 90°.
Пояснення:
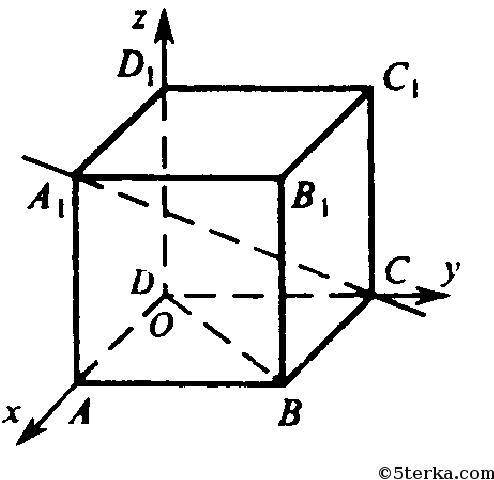
Пусть дан куб ABCDА1B1C1D1, А1С — диагональ куба; DB — диагональ грани куба.
Введем прямоугольную систему координат. С началом координат в т. D и осями, направленными вдоль ребер ОА, ОВ, ОС. Обозначим сторону куба через а.
https://ru-static.z-dn.net/files/db8/7fabd2e163d548ee435973a4d2fc01c5.png
Тогда
1.
https://ru-static.z-dn.net/files/d03/960059a78aaeb368ff09035647522aff.png
2.
https://ru-static.z-dn.net/files/d84/f0e867a68ec10485951a3ce407b94813.png
3.
https://ru-static.z-dn.net/files/d65/90661f99b8c5653eccbb98e37e38d02e.png
Следовательно,
https://ru-static.z-dn.net/files/d73/59578781fa9cf36028faf845653e9834.png
соответственно угол между прямыми
A1C и DB равен 90°.
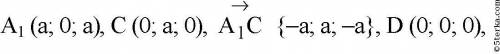
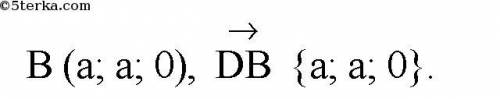
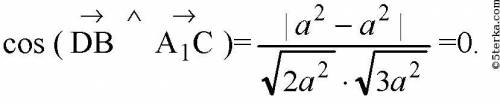
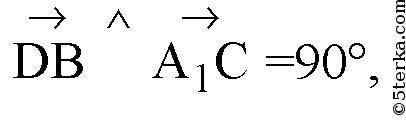
по т. пифагора
AC=корень (29*29-20*20)=21