Нарисуем этот треугольник.
Обозначим точки буквами- см.рисунок.
Получились прямоугольные треугольники, высоты в который определяются по формуле высоты равностороннего треугольника
h=(а√3):2
Найдем сторону ВК в треугольнике КВМ
3=(ВК√3):2
(ВК√3)=3*2=6
ВК=6:√3=2√3
По той же формуле найдем АВ
5=(АВ√3):2
АВ√3=5*2=10
АВ=10:√3=(10√3):3
АК=(10√3):3 -2√3=(10√3 -6√3):3=(4√3):3
КН=√3(4√3):3):2=12:6=2см
рисунок - во вложении
----------------------------------------------
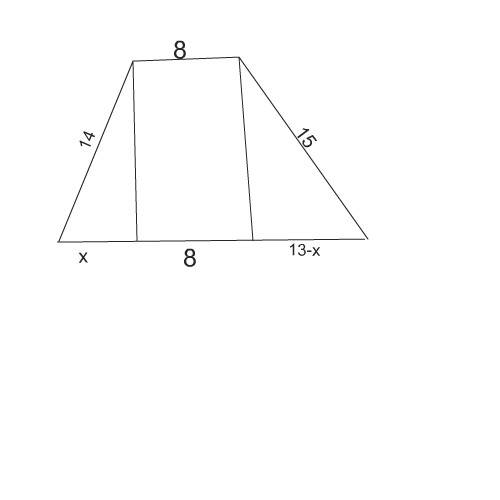
Рисуем трапецию.
Опустим из ее углов при меньшем основании высоты на нижнее основание.
Получили один прямоугольник и два прямоугольных треугольника при боковых сторонах как гипотенузах.
Найдем значение высот и приравняем их.
Для этого отрезок основания при боковой стороне 14 обозначим х, а отреок ( катет) при боковой стороне 15 будет 21-х-8=13-х
14²-х²=15²-(13-х)²
Из этого уравнения найти х, затем из прямоугоьного треугольника с гипотенузой 14 и катетом, равным найденному х, вычислить высоту трапеции.
1) 3 см
2) ≈ 28°
3) ≈ 37°
4) 144 см²
Объяснение:
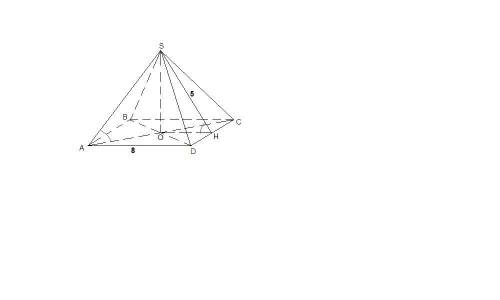
Пирамида правильная, значит основание - квадрат, боковые грани - равные равнобедренные треугольники, высота проецируется в центр основания - точку пересечения диагоналей квадрата.
SO - высота пирамиды.
∠SAO - угол наклона бокового ребра к плоскости основания (так как АО - проекция ребра SA на плоскость основания)
Пусть Н - середина CD, тогда SH - медиана и высота равнобедренного треугольника SCD, т.е. апофема пирамиды.
∠SHO - угол наклона боковой грани к плоскости основания (так как SH⊥CD и ОН⊥CD по теореме, обратной теореме о трех перпендикулярах)
1) SH = 5 см
OН = AD/2 = 4 см как средняя линия треугольника ACD.
ΔSOH: (∠SOH = 90°), по теореме Пифагора
SO = √(SH² - OH²) = √(5² - 4²) = 3 см
sin∠SHO = SO/SH = 3/5 = 0,6
3) ∠SHO = arcsin 0,6 ≈ 37°
2) AC = AB√2 как диагональ квадрата,
АС = 8√2 см, АО = АС/2 = 4√2 см
ΔSAO: (∠SOA = 90°),
tg∠SAO = SO/AO = 3 / (4√2) = 3√2/8
∠SAO = arctg 3√2/8 ≈ 28°
4) Sполн = Sосн + Sбок
Sосн = АВ² = 8² = 64 см²
Sбок = 1/2 Pосн · SH = 1/2 · 4 · 8 · 5 = 80 см²
Sполн = 64 + 80 = 144 см²
угол, из которого проведена высота=120°