Үшбұрыштың теңдік белгілері.
1. Егер бірінші үшбұрыштың екі қабырғасы мен олардың арасындағы бұрышы екінші үшбұрыштың сәйкес екі қабырғасы мен арасындағы бұрышқа тең болса, онда бұл үшбұрыштар тең болады.
2. Егер бірінші үшбұрыштың бір қабырғасы және оған іргелес жатқан екі бұрышы екінші үшбұрыштың сәйкес қабырғасы мен оған іргелес жатқан екі бұрышына тең болса, онда бұл үшбұрыштар тең болады.
3. Егер бір үшбұрыштың үш қабырғасы екінші үшбұрыштың сәйкес үш қабырғасына тең болса, онда бұл үшбұрыштар тең болады.
Объяснение:
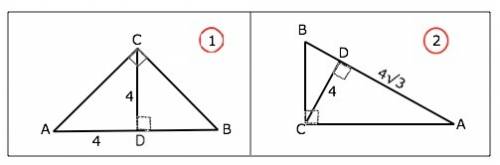
Найдем второй отрезок гипотенузы для каждого случая.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.⇒
a)
СD²=АD•ВD
16=4•BD
BD=16:4=4⇒
Высота СD - медиана и биссектриса ∆ АВС и делит его на два равнобедренных прямоугольных треугольника.
Острые углы такого треугольника равны 45°
б)
СD²=АD•ВD
16=4√3•BD⇒
BD=16:4√3=4/√3
Из ∆ САD:
tg∠САD=CD:AD=4:4√3=1/√3- это тангенс 30°
Из ∆ CВD:
tg∠СBD=BD:CD=(4/√3):4=√3 - это тангенс 60°
Острые углы этого треугольника 30° и 60°