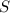данного сечения = 
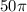ед.кв.
Объяснение:
Пусть будет дан шар с центром в точке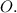 
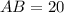ед.
Через точку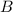 
проведём плоскость под углов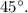 
Пусть будет плоскость с центром в точке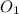 
.
Тогда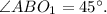 
========================================================
Так как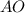 
и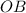 
- радиусы данного шара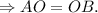 
Т.е.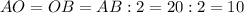 
ед.
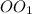
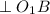, так как 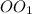- серединный перпендикуляр.
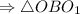- прямоугольный.
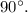
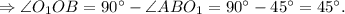
Так как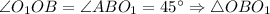 
- равнобедренный.
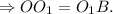
Пусть 
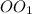- и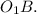 
По теореме Пифагора:
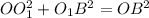
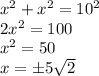
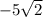- отрицательное число, поэтому не подходит.
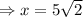
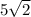ед. -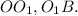 
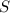данного сечения = 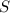круга = 
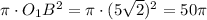ед.кв.
Угол между векторами равен arccos(0,316) ≈ 71,58°.
Объяснение:
Угол α между векторами a и b вычисляется по формуле:
cosα=(Xa*Xb+Ya*Yb)/[√(Xa²+Ya²)*√(Xb²+Yb²)].
В нашем случае:
скалярное произведение Xa*Xb+Ya*Yb = -1+2 = 1.
произведение модулей векторов:
√(Xa²+Ya²)*√(Xb²+Yb²) = √(1+4)*√(1+1) = √10.
cosα = 1/√10 = √10/10 ≈ 0,316.
Угол между векторами равен arccos(0,316) ≈ 71,58°.