Прямые BD и m - скрещивающиеся прямые.
Объяснение:
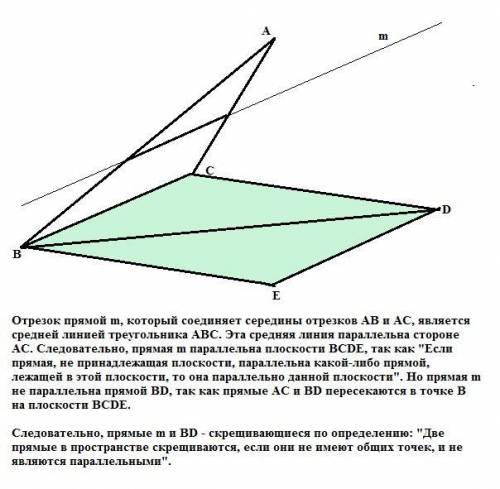
Отрезок прямой m, который соединяет середины отрезков AB и AC, является средней линией треугольника АВС. Эта средняя линия параллельна стороне АС. Следовательно, прямая m параллельна плоскости ВСDE, так как "Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельно данной плоскости". Но прямая m не параллельна прямой BD, так как прямые АС и BD пересекаются в точке В на плоскости BCDE.
Следовательно, прямые m и BD - скрещивающиеся по определению: "Две прямые в пространстве скрещиваются, если они не имеют общих точек, и не являются параллельными".
1) угол 5 = угол 8 = угол 1 = угол 4 = 124 градуса
угол 6 = угол 7 = угол 2 = угол 3 = 180-124=56 градусов
2) угол 2 = угол 3 (если смотреть по первому рисунку, на этом рисунке обозначеия нет) = 180 — угол 1
т.е. угол 6 + угол 1 = 180
если сумма внутренних односторонних углов равна 180 градусов, значит прямые параллельны
3) угол 1 = угол 4 (если смотреть номера по первому рисунку) — они вертикальные
угол 1 = угол 4, значит угол 4+угол 2=180 градусов
если сумма внутренних односторонних 180, значит а и b параллельны
угол 2 = угол 3 — соответствующие
если соответствующие углы равны, значит b и с параллельны
т.к. a параллельна b и с параллельна b, значит а параллельна с
остроугольные
прямоугольные
тупоугольные
виды по сторонам :
равносторонние
равнобедренные
разносторонние