Площадь круга, как Вы помните, находят по формуле
S=πr²
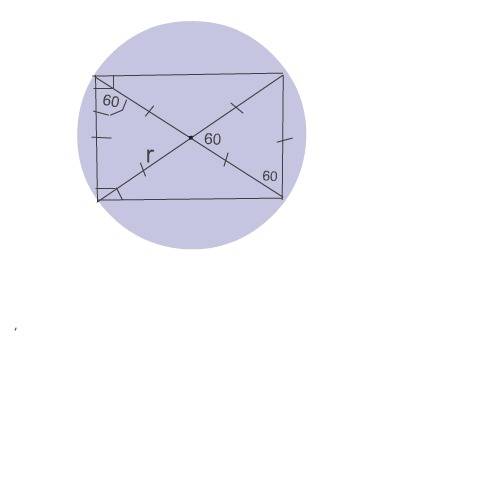
Радиус находим из остроугольных треугольников, образовавшимися диагоналями при меньшей стороне прямоугольника.
Эти треугольники - равносторонние, т.к. угол при пересечении диагоналей равен 60°, а сами диагонали делятся пополам и этим образуют равнобедренные треугольники, углы которых при основании, равном меньшей стороне вписанного прямоугольника, тоже равны 60°.⇒cледовательно, каждая половина диагонали равна меньшей стороне прямоугольника. А так как диагонали здесь являются диаметрами окружности, то радиус описанного круга тоже равен меньшей стороне прямоугольника.
r=10 см
S=πr²,
S=100 π см²
Для начала построим треугольник АВС.
Отрезок ВС - часть стороны искомого треугольника, противоположной вершине А, поэтому смело рисуем всю прямую ВС.
Вспоминаем, как ведём себя биссектриса во вписанном треугольнике. Она пересекает дугу описанной окружности, отсечённую противоположной стороной, посередине. так как на равные половинки этой дуги опираются равные вписанные углы, образованные биссектрисой из угла происхождения.
Одновременно, срединный перпендикуляр хорды проходит не только через центр описанной окружности, но и делит дуги окружности, образованные хордой, пополам, значит продолжение биссектрисы АВ и срединный перпендикуляр к стороне треугольника, содержащей отрезок ВС, пересекаются на описанной окружности.
Точка С - середина будущей стороны искомого треугольника. Проведём через неё перпендикуляр прямой ВС, который пересечётся с биссектрисой АВ в точке Д.
Прямая СД проходит через центр описанной окружности, а АД - хорда.
Срединный перпендикуляр к хорде АД даст нам точку Е - пересечение со срединным перпендикуляром будущей стороны искомого треугольника. Е - центр описанной окружности, проходящей через точки А и Д. Строим её, получаем точки F и G на прямой ВС.
Дуги FD и GD равны, значит ∠FAB=∠GAB.
FC=CG.
ΔAGF - наш треугольник.