R=5 см
Объяснение:
маємо коло , дві паралельні хорди 6 см і 8 см відстань між хордами 7 см , треба знайти радіус кола Рішення: Через центр 0 проведемо діаметр , який пересіче навпіл малу і велику хорди. З центра 0 проведемо до точок перетину хорд з колом два радіуси і отримаємо два прямокутних трикутника. Щоб знайти радіуси , які є діагоналями цих трикутників, треба розвязати систему. Нам відомо, що відстань між хордами 7 см і не відомо , яка відстань центру кола від хорд. Позначимо одну відстань від центру кола до малої хорди через Х, тоді друга відстань від центра до великої хорди буде 7-Х. складемо систему : R1=R2
R1²=Х²+3² R2²=(7-Х)²+4² х²+9=49-14Х+Х²+16 14Х=56 Х=4
тобто діаметр , або 2 радіуси роздвлили відстань між хордами на 3 і 4 см. тепер ми знайдемо радіус , використовуючи теорему Піфагора, R²=4²+3²=25√=5
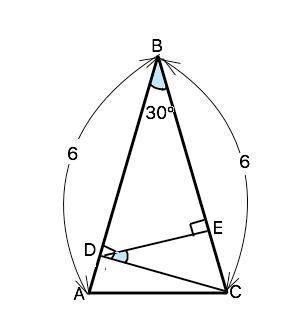
В равнобедренном треугольнике ABC угол В равен 30°, AB=BC=6, проведены высота CD треугольника ABC и высота DE треугольника BDC. Найдите BE.
——————————
ответ: 4,5 (ед. длины)
Объяснение:
Из ∆ ВDC катет DC противолежит углу 30° ⇒ DC=ВС:2= 6:2=3 (свойство).
Высота прямоугольного треугольник, проведенная к гипотенузе, делит его на треугольники, подобные друг другу и исходному треугольнику. Сумма острых углов прямоугольного треугольника 90°.
Угол BСD=90°-∠DBC=90°-30°=60°, угол ЕDC=30°.
CD - гипотенуза прямоугольного ∆ СЕD, катет ЕС противолежит углу 30°,⇒ ЕС=СD:2=3:2=1,5 ⇒
ВЕ=6-1.5=4,5
Или:
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией катета на неё.
СD²=BC•EC. Из найденного СD=3.
3²=6•CE ⇒ CE=1,5 a BE=BC-CE=6-1,5=4,5
1. 10 см, 6 см, 8 см существует
2. 7 см, 3 см, 3 см не существует, т.к. 3+3<7
3. 54 см, 30 см, 20 см не существует, т.к. 30+20<54
4. 40 см, 40 см, 90 см не существует, т.к. 40+40<90