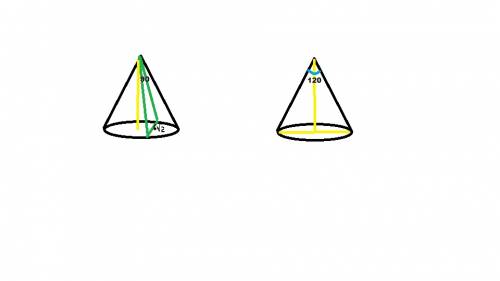
Образующая AS, как катет равнобедренного прямоугольного треугольника ASВ c прямым углом при вершине S и с гипотенузой АВ=6√2, равна 6 см
Высота SО, как катет прямоугольного треугольника ASО с прямым углом при основании высоты, равна половине АS, так как противолежит углу 30°
h=AS:2=3 см
Радиус r основания конуса найдем из треугольника АSO. Можно по теореме Пифагора или через косинус угла SАО.
АО=r=АS·cos(30°)=6·√3):2=3√3
Объем конуса равен одной трети произведения площади основания на его высоту и находится по формуле:
V= π r² H:3
V==π 27·3 : 3=27π см³
1. Диаметр = 2*Радиус = 2* 2.5 см = 5 см
Диаметр - это максимально возможная хорда, проходящая через центр,
значит, если диаметр=5см, то хорда не может быть равна 6 см (выходит за пределы окружности)
2. Две окружности касаются, если расстояние между их центрами равно сумме их радиусов.
Если сумма радиусов меньше - то не пересекаются
Если сумма радиусов больше - то они пересекаются, а не касаются!
Р1+Р2 = 25+50 = 75 см,что больше расстояния между центрами окружностей
Значит окружности пересекаются, а не КАСАЮТСЯ!
Удачи!
1) ∠О = 90° (ВС=h ⊥ основанию конуса) ⇒ ΔАОВ -прямоугольный
2) Сумма острых углов прямоугольного треугольника равна 90 °, следовательно:
∠ В = 90 - ∠ А ⇒ ∠В = 90 - 45 = 45° ⇒
ΔАОВ - равнобедренный, следовательно:
∠А=∠В = 45° (углы при основании АВ)
ВО=АО =r = 13 см ( боковые стороны)
⇒ АО = h = 13 см
ответ : h = 13 см.