α = 45°
Объяснение:
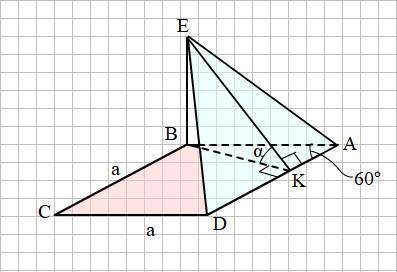
Смотри прикреплённый рисунок.
Из вершины В ромба проводим высоту ВК.
ВК = а · sin A = a · sin 60° = 0.5a√3.
Соединим точку Е с точкой К. ВК является проекцией наклонной ЕК на плоскость АВСD. Поскольку ВК - высота ромба. то ВК ⊥ AD.
По теореме о трёх перпендикулярах: если AD ⊥ BK (проекции наклонной ЕК), то AD⊥ ЕК. Следовательно, ∠ЕКВ = α является линейным углом, служащим мерой двугранного угла между плоскостями ADE и АВСD.
Найдём этот угол.
tg α = BE : BK = 0.5a√3 : 0.5a√3 = 1.
Следовательно, ∠α = 45°
если G - точка пересечения медиан. На самом деле это соотношение можно вообще считать определением, но и в обычном школьном определении это тривиально показать, так как
GA + GB = 2*GM = - GC;
где M - середина AB
Тогда
3*PG = PA + PB + PC; (2)
для любой точки P - это сразу видно, если подставить
PA = PG + GA; PB = PG + GA; PC = PG + GC;
Из (1) после возведения в квадрат
0 = GA^2 + GB^2 + GC^2 + 2(GA*GB +GA*GB + GB*GC); (3)
а из (2)
9*PG^2 = PA^2 + PB^2 + PC^2 + 2(PA*PB + PA*PC + PB*PC) =
PA^2 + PB^2 + PC^2 + 2((PG + GA)*(PG + GB) + (PG + GA)*(PG + GC) + (PG + GB)*(PG + GC)) = PA^2 + PB^2 + PC^2 + 6*PG^2 + 4*PG*(GA + GB + GC) + 2(GA*GB + GA*GC + GB*GC);
если учесть (1) и (3), получается
3*PG^2 = PA^2 + PB^2 + PC^2 - (GA^2 + GB^2 + GC^2)
Везде жирным шрифтом обозначены вектора, а PA*PB означает в этих случаях скалярное произведение.
ЧТД