Данные диагонали пересекаются в одной точке и составляют 4 прямоугольных угла. Можем найти их углы по определению синуса (отношение противолежащего катета к гипотенузе) и косинуса (отношение прилежащего катета к гипотенузе), а стороны (гипотенузы) по теореме Пифагора.
Известны катет a= 5 и катет b = 12
Найдем гипотенузу прямоугольного треугольника. Для этого воспользуемся формулой Пифагора:
c ²=а²+b²
Тогда:
c = √ a²+b²
Подставляя значения a и b, получим:
c = √ ( 5 )² + ( 12 ) ²=13
Найдем, далее, острые углы прямоугольного треугольника
s i n A = a c = 5 *13 = 0.38
Отсюда:
∠ A = a r c s i n( 0.38 ) = 22.33 °
Найдем угол B:
∠ B = 90 ° − ∠ A = 67.67°
В итоге, я узнала, что углы одного из четырех треугольников, на которые был разделен ромб, равны 90°;67,67°; 22,33°. Т.к. эти диагонали являлись также и биссектрисами, то мы умножим на 2 углы. Таким образом, у ромба 2 угла по 135,34° и 2 угла по 44,66°
168 кв ед
Объяснение:
1)Рассмотрим прямоугольный треугольник АВН(<Н=90°)
<В=90°-45°=45° => треугольник АВН - равнобедренный. АН=ВН=24
Площадь прямоугольного треугольника равна половине произведения его катетов :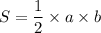
а=АН=24, b=ВН=24
тогда площадь треугольника АВН равна:
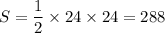
2)Рассмотрим прямоугольный треугольник CВН(<Н=90°)
По теореме Пифагора найдём катет СН:
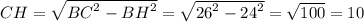
Площадь треугольника СВН(катет а=СН=10, катет b=ВН=24):
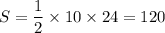
Площадь треугольника ABC равна разности площадей треугольников АВН и СВН:
S(ABC)=S(ABH)-S(CBH)=288-120=168 кв ед.
tg B=AC/BC=8/10=0,8