Диагонали параллелограмма точкой пересечения делятся пополам, а по условию они пересекаются под прямым углом.
Тогда в прямоугольных треугольниках, на которые диагонали делят данный параллелограмм, меньшие катеты равны половине меньшей диагонали, большие катеты равны половине большей диагонали. Если в прямоугольных треугольниках катеты равны, то равны и треугольники. Следовательно, равны и их гипотенузы. А гипотенузы этих треугольников - стороны данного параллелограмма.
Если все стороны параллелограмма равны - этот параллелограмм - ромб.
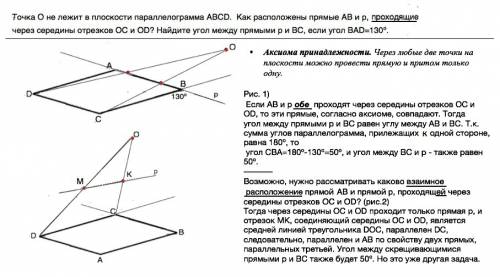
Точка О не лежит в плоскости параллелограмма ABCD. Как расположены прямые AB и p, проходящие через середины отрезков OC и OD? Найдите угол между прямыми p и BC, если угол BAD=130º
––––––––––––
Аксиома . Через любые две точки на плоскости можно провести прямую и притом только одну.. Если АВ и р обе проходят через середины отрезков ОС и ОD, то эти прямые, согласно аксиоме, совпадают. Тогда угол между прямыми р и ВС равен углу между АВ и ВС. Т.к. сумма углов параллелограмма, прилежащих одной стороне, равна 180º угол СВА=180º-130º=50º
–––––––
Возможно, нужно рассматривать каково взаимное расположение прямой AB и прямой p, проходящей через середины отрезков OC и OD, но расположенной в другой плоскости?
Тогда через середины ОС и ОD проходит только прямая р, и отрезок МК, соединяющий середины ОС и ОD, является средней линией треугольника DОC, параллелен DC, следовательно, параллелен и АВ по свойству двух прямых, параллельных третьей. Угол между скрещивающимися прямыми р и ВС также будет 50º. Но это уже другая задача.