
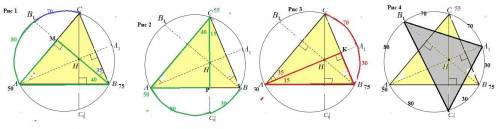
Ортоцентр H треугольника ABC отразили относительно сторон и получили точки A₁, B₁ и C₁. Найдите углы треугольника A′B′C′, если ∠A=50∘, ∠B=75∘.
Объяснение:
По свойству ортоцентра : "Точка, симметричная ортоцентру относительно стороны треугольника, лежит на описанной около него окружности". Значит все точки А, В, С,A₁, B₁ , C₁-лежат на окружности.
1)ΔАВМ -прямоугольный ,∠А=50°⇒ ∠АВМ=90°-50°=40° . Значит ∠МВС=75°-40°=35° .Поэтому дуги ∪ АВ₁=80° и ∪ В₁С=70° по т. о вписанном угле.
2)ΔАСР -прямоугольный ,∠А=50°⇒ ∠АСР=90°-50°=40° . Значит ∠РСВ=55°-40°=15° .Поэтому дуги ∪ АС₁=80° и ∪ С₁В=30° по т. о вписанном угле.
3)ΔАВК -прямоугольный ,∠В=75°⇒ ∠ВАК=90°-75°=15° . Значит ∠САК=50°-15°=35° .Поэтому дуги ∪ СА₁=70° и ∪ А₁В=30° по т. о вписанном угле.
)ΔА₁В₁С₁ , по т. о вписанном угле : ∠А₁=1/2*(80°+80)°=80° ,∠В₁=1/2*(30°+30)°=30° , ∠С₁=1/2*(70°+70)°=70°.
Т.к. треугольники равнобедренные, то АВ=ВС и А1В1=В1С1. По условию АВ=А1В1, а значит АВ=ВС=А1В1=В1С1.
Рассмотрим треугольники АВК и АВК1. ВК=В1К1(т.к. К и К1 середины сторон ВС и В1С1 соответственно(по условию)),АВ=А1В1, АК=А1К1(по условию)===>треугольники равны по трём сторонам. Поэтому у них равны и углы: угол В=угол В1.
Рассмотрим треугольники АВС и А1В1С1. АВ=А1В1, ВС=В1С1, угол В=угол В1. Треугольники АВС равен треугольнике А1В1С1 по 2 сторонам и углу между ними.
Доказано.
Будуто вопросы обращайся.