решение представлено на фото
Объяснение:

ответ: S тр. ABCD = 300 ед.кв.
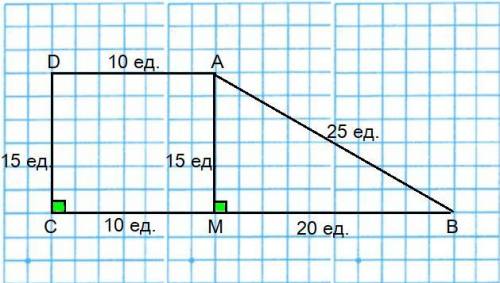
Объяснение: Проведём из т.A к большему основанию BC высоту AM.
Отрезок DC не только боковая сторона прямоугольной трапеции ABCD, но и высота этой трапеции.
DC ⊥ BC; AM ⊥ BC ⇒ DC ║ AM ⇒ CD = AM = 15 ед.
Т.к. AM - высота ⇒ ΔAMB - прямоугольный.
Найдём катет MB по т.Пифагора:
MB = √(AB² - AM²) = √(25² - 15²) = √(625 - 225) = √400 = 20 ед.
CM = AD, т.к. AM отсекает от трапеции ABCD прямоугольник DAMC.
Пусть x ед. меньшее основание трапеции (AD), тогда (x+20) ед. равно большее основание трапеции (BC). AB+BC+CD+AD=80 ед.
25 + (x + 20) + 15 + x = 80; 60 + 2x = 80; 2x = 20; x = 10
Если меньшее основание AD прямоугольной трапеции ABCD составляет 10 ед. ⇒ большее основание BC = 30 ед.
Формула площади нашей прямоугольной трапеции : (AD+BC)/2*AM.
⇒ S тр. ABCD = (10 + 30)/2 * 15 = 40/2 * 15 = 20 * 15 = 300 ед.кв.
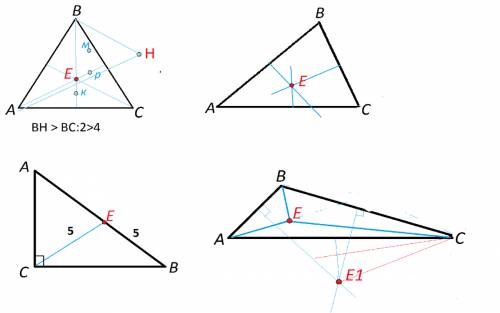
S(DAEC) = 24
Объяснение:
Смотри прикреплённый рисунок
Обозначим: АВ = а; ВС = b; BE = AE = 0.5AB = 0.5a;
Площадь параллелограмма S(ABCD) = AB · BC · sin B = ab · sin B = 32
Площадь треугольника СВЕ равна S(CBE) = 0.5 BE · BC · sin B = 0.5 · 0.5a · b · sin B = 0.25 a· b · sin B = 0.25 S(ABCD)
Площадь трапеции DAEC равна
S(DAEC) = S(ABCD) - S(CBE) = S(ABCD) - 0.25 S(ABCD) = 0.75 S(ABCD) =
= 0.75 · 32 = 24