ответ: 20 см
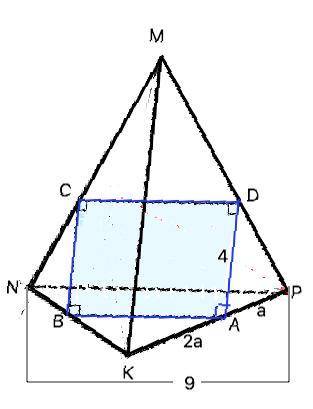
Объяснение: Рассмотрим основание NPK данного тетраэдра. Сторона АВ получившегося прямоугольника параллельна стороне PN треугольника NPK. Треугольники КВА и КNP подобны по двум углам: угол К общий, углы КАВ и КРN равны как соответственные при пересечении параллельных АВ и PN секущей КР.
Из данного в условии отношения отрезков ребра РК примем РА=а, АК=2а, ⇒ РК=РА+АК=а+2а=3а. Коэффициент подобия РК:АК=3:2 . ⇒ PN:АВ=3:2, откуда АВ=2/3 PN=9•2/3=6 дм.
Противоположные стороны прямоугольника равны. Р(АВСD)=2•(АВ+АD)=2•(6+4)=20 (см)
1. При сечении пирамиды плоскостью, перпендикулярной основанию и проходящей через вершину, линия пересечения плоскости сечения и плоскости, содержащей основание, проходит через точку основания высоты пирамиды и через две противоположные точки, находящиеся на линиях пересечения двух противоположных боковых граней пирамиды. То есть плоскость сечения проходит через три общих с пирамидой точки, а фигура, состоящая из трех прямых, пересекающихся в трех точках - треугольник.
ответ: а) - треугольник
2. Плоскость сечения пересекает параллельные плоскости по параллельным прямым. Значит линии пепесечения оснований цилиндра с плоскостью сечения параллельные и равные отрезки (так как основания цилиндра - параллельные круги равных диаметров, а образующие цилиндра перпендикулярны основаниям). Фигура сечения - прямоугольник по определению, так как имеет пары параллельных и равных сторон.
ответ: а) - прямоугольник
3. Сечение конуса плоскостью, параллельной основанию, пересекает конус по линии, параллельной основанию, то есть по линии, все точки которой равноудалены от линии основания. Следовательно, плоскость сечения - круг, подобный кругу основания.
ответ: г) - круг