 , то другая следовательно тоже равна
, то другая следовательно тоже равна  . Так как у нас диагональ перпендикулярна, иными словами под 90 гр, то пусть большое основание равна
. Так как у нас диагональ перпендикулярна, иными словами под 90 гр, то пусть большое основание равна 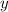 , тогда справедлива теорема Пифагора !
, тогда справедлива теорема Пифагора ! 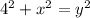
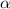 , то другой угол равен
, то другой угол равен  , и пусть угол при меньшем оснований равны
, и пусть угол при меньшем оснований равны 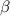 ,то в сумме
,то в сумме 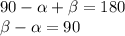
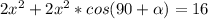
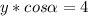
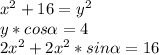
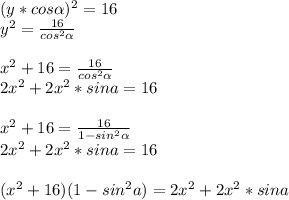
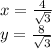
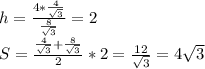

Величину его х находим по свойству высоты из вершины прямого угла.
х = √(3*12) = √36 = 6 см.
Высота ромба равна 2*6 = 12 см.
Сторона ромба равна 3 + 12 = 15 см.
Площадь ромба равна 15*12 = 180 см².