Вравнобедренный прямоугольный треугольник вписана окружность радиуса 9. вторая окружность касается катетов треугольника и первой окружности. найти радиус второй окружности.

👇

Ответ:

wigswond

31.08.2022

Проведем из центров окружностей радиусы в точки касания окружностей с катетами. Они перпендикулярны катетам.
Получились квадраты СКОН и CFO'E, стороны которых равны 9 и r соответственно.
Проведем O'H'║EH.
OO' = 9 + r
OH' = O'H' = 9 - r
Из треугольника OH'O' (∠OH'O' = 90°) по теореме Пифагора составим уравнение:
(OO')² = (OH')² + (O'H')²
(9 + r)² = (9 - r)² + (9 - r)²
81 + 18r + r² = 2(81 - 18r + r²)
81 + 18r + r² = 162 - 36r + 2r²
r² - 54r + 81 = 0
D/4 = 27² - 81 = 648
r = 27 + 18√2 или r = 27 - 18√2
В первом случае радиус маленькой окружности приблизительно равен 52,5, что невозможно по условию задачи, во втором ≠ 1,5.
ответ: 27 - 18√2

4,5(27 оценок)

Открыть все ответы

Ответ:

Smal1488

31.08.2022

Будем использовать следующие значения для сторон треугольника АВС: АВ=с, ВС=а, СА=b и его углов:

<А=а, <В=b, <C=y (a, b, y : Альфа, Бэта, Гама.)

Дано:

а=4, b=5, c=6.

Найти: a, b, y -?

Пусть b - наибольшая сторона, b<a+c.

По теореме косинусов находим наибольший угол b,

[Не обязательно писать, для ориентира: Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.]

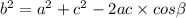
${b}^{2} = {a}^{2} + {c}^{2} - 2ac \times cos \beta$

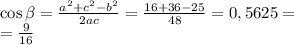
$\cos\beta = \frac{a {}^{2} + c {}^{2} - b {}^{2} }{2ac} = \frac{16 + 36 - 25}{48} = 0,5625 = \\ = \frac{9}{16}$

При основного тригонометрического тождества найдём Sin B

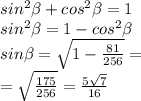
$sin {}^{2} \beta + cos {}^{2} \beta = 1 \\ sin {}^{2} \beta = 1 - cos {}^{2} \beta \\ sin \beta = \sqrt{1 - \frac{81}{256} } = \\ = \sqrt{ \frac{175}{256} } = \frac{5 \sqrt{7} }{16}$

С теоремы синусов найдём углы треугольника:

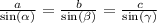
$\frac{a}{ \sin( \alpha ) } = \frac{b}{ \sin( \beta ) } = \frac{c}{ \sin( \gamma ) }$

Отсюда,

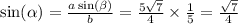
$\sin( \alpha ) = \frac{a \sin( \beta ) }{b} = \frac{5 \sqrt{7} }{4} \times \frac{1}{5} = \frac{ \sqrt{7} }{4}$

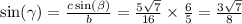
$\sin( \gamma ) = \frac{c\sin( \beta ) }{b} = \frac{5 \sqrt{7} }{ 16} \times \frac{6}{5} = \frac{3 \sqrt{7} }{8}$

С таблиц находим градусную меру углов:

а≈41°

b≈57°

Тогда,

у≈82°

ответ: 41° 57° 82°

4,5(15 оценок)

Ответ:

anastasiaselina

31.08.2022

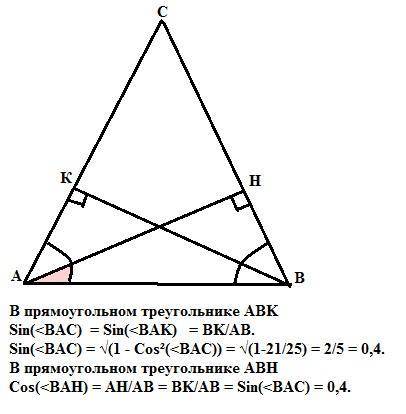
В равнобедренном треугольнике АВС высоты АН и ВК, проведенные к боковым сторонам ВС и АС соответственно, равны. Это равенство вытекает из равенства прямоугольных треугольников АВН и АВК по острому углу (<B=<A как углы при основании треугольника АВС) и гипотенузе (АВ - общая).

В прямоугольном треугольнике АВK

Sin(<BAC)=Sin(<BAK)=BK/AB.

Sin(<BAC) = √(1 - Cos²(<BAC)) = √(1 - 21/25) = 2/5 = 0,4.

В прямоугольном треугольнике АВH, так как АН=ВК,

Cos(<BAH) = AH/AB = BK/AB = Sin(<BAC) = 0,4.

ответ: Cos(<BAH) = 0,4.