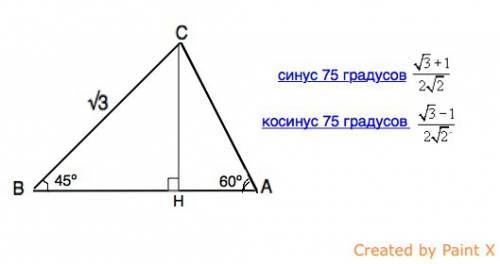
Решением треугольника называется нахождение всех его шести элементов (т. е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
Из суммы углов треугольника найдем угол С:
∠С=180º-45º-60º=75º
В прямоугольном ⊿ ВНС угол ВСН=90º-45º=45º
⊿ ВНС - равнобедренный, СН=ВН=ВС•sin 45º=(√3•√2):2
В ⊿ АНС сторона АС=СH:sin 60º
AC=[(√3•√2):2]:(√2):2=√2
АВ=ВН+АН
АН противолежит углу НСА, равному 90º-60º=30º
АН=АС:2=(√2):2
АВ=(√3•√2):2+(√2):2=(√3+1):√2
––––––––––––
Или по т. синусов:
АВ:sin75=BC:sin60
sin 60º=(√3):2
sin 75º=(√3+1):2√2 ( из таблицы тригонометрических функций)
АВ:(√3+1):2√2=(√3):[(√3):2]⇒
AB=(√3+1):√2
--------------
или по т.косинусов
AB²=BC²+AC²- 2BC•AC•cos75º
cos 75º=(√3-1):2√2
AB²=3+2- 2√6•((√3-1):2√2)⇒
AB=√(2+√3)
Оба найденных значения АВ равны - проверьте, возведя их в квадрат.
[√(2+√3)]²=[(√3+1):√2]²
РЕШЕНИЕ
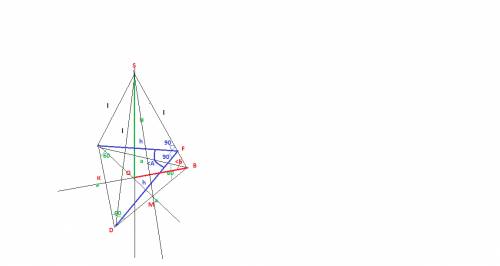
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
-боковые ребра правильной пирамиды равны;
-все боковые грани — равные равнобедренные треугольники
высота пирамиды Н=l*sin(b)
основание пирамиды равносторонний треугольник
все углы равны - 60 град
все стороны равны -а
ВК - медиана, биссектриса, высота
ВО=l*cos(b)
BO=2/3*BK
BK=3/2*BO=3/2* l*cos(b)
сторона основания a =BK/sin60=3/2* l*cos(b)/(√3/2)= √3*l*cos(b)
высота боковой грани SM=√(SB^2-MB^2)=√(l^2-(a/2)^2)=√(l^2-((√3*l*cos(b))/2)^2)=
=1/2*l*√(4-3cos^2(b))
выразим ПЛОЩАДЬ треугольника SDB
- через ВЫСОТУ и ОСНОВАНИЕ двумя тогда имеем отношение BD*SM =SB*DF => DF= BD*SM /SB
h=DF=a* 1/2*l*√(4-3cos^2(b)) / l =√3*l*cos(b) *1/2*l*√(4-3cos^2(b)) / l=
=√3/2 *l*cos(b)√(4-3cos^2(b))
теорема косинусов
a^2 = h^2+h^2-2h^2*cosA =2h^2(1-cosA)
cosA=1 - a^2 / (2*h^2)
cosA =1- (√3*l*cos(b))^2 / (2*√3/2 *l*cos(b)√(4-3cos^2(b)))^2 = 1 - 1 / (4-3cos^(b))
A = arccos (1 - 1 / (4-3cos^(b)) )
ответ < A = arccos (1 - 1 / (4-3cos^(b)) ) ; Н=l*sin(b)