Для прямоугольного треугольника справедлива теорема Пифагора : квадрат гипотенузы равен сумме квадратов катетов.
Треугольник с заданными сторонами является прямоугольным.
25² = 7² + 24²
625 = 49 + 576 = 625
Пусть коэффициент пропорциональности равен k, тогда пропорциональные стороны треугольника будут 7k, 24k, 25k
(25k)² = (7k)² + (24k)²
625k² = 49k² + 576k² ⇒ 625k² = 625k²
Для треугольника со сторонами 7k, 24k, 25k тоже справедлива теорема Пифагора, значит, треугольник является прямоугольным.
1.
Дано: Δ АВС, S=9√3 cм², АВ=12 см, АС=3 см. Найти ∠ВАС.
Решение: угол ВАС найдем из формулы площади треугольника S=1\2a*b*sinα
9√3=1\2 * 12 * 3 * sinВАС
18sinВАС=9√3, sinВАС=√3\2, ∠ВАС=60°.
ответ: 60°.
2.
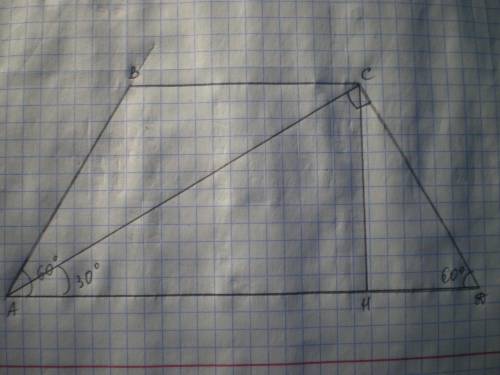
Дано: АВСД - трапеция, АВ=СД, АД=20√3, ∠А=∠Д=60°, АС⊥СД. Найти S(АВСД).
Решение: Проведем высоту СН, тогда S(АВСД)=(ВС+АД):2*СН.
Рассмотрим ΔАСД - прямоугольный, ∠Д=60°, тогда ∠САД=90-60=30°, а СД=1\2 АД=20√3:2=10√3.
Диагональ АС перпендикулярна к боковой стороне и делит угол А пополам, значит большее основание трапеции в два раза больше меньшего основания и её боковых сторон; и высота трапеции равна половине её диагонали.
СД=ВС=20√3:2=10√3;
АС²=(20√3)²-(10√3)²=1200-300=900; АС=√900=30.
СН=1\2 АС=30:2=15.
S(АВСД)=(20√3+10√3):2*15=225√3 (ед²).
ответ: 225√3 ед²
Смежные углы составляют развёрнутый угол, 180.
AOB+BOC =180 => AOB/2 +BOC/2 =90
Биссектриса делит угол пополам.
MOB=AOB/2
MOB+BON =90 => AOB/2 +BON =90 => BON=BOC/2
Луч ON делит угол BOC пополам, следовательно является его биссектрисой.
Биссектрисы смежных углов перпендикулярны.