Теоремы (свойства параллелограмма):
В параллелограмме противоположные стороны равны и противоположные углы равны: AB = CD, BC = AD, \angle ABC = \angle
ADC,\angle BAD = \angle BCD.
Диагонали параллелограмма точкой пересечения делятся пополам: AO
= OC, OB = OD.
Углы, прилежащие к любой стороне, в сумме равны 180^\circ .
Диагонали параллелограмма делят его на два равных треугольника.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: AC^2 + BD^2 = 2AB^2 + 2BC^2 .
Признаки параллелограмма:
Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника K,\;L,\;M,\;N являются вершинами параллелограмма Вариньона.
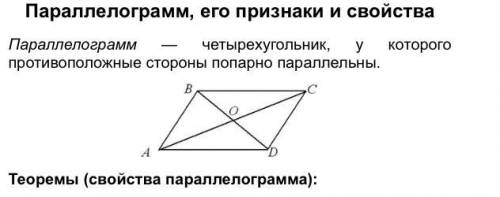
В прямокутному трикутнику катет довжиною 15 см прилягає к куту 30°. Знайдіть бісектрису другого гострого кута цього трикутника.
В прямоугольном треугольнике катет длиной 15 см прилегает к углу 30 °. Найдите биссектрису второго острого угла этого треугольника.
Дано :
∠C =90° ;
AC =15 см ;
∠A =30 ° ;
∠ABD =∠CBD = ∠ABC /2 ( BD _биссектриса )
-----------------
BD - ?
∠ABC = 90° - ∠ A =90° -30° =60°
∠ABD =∠CBD = ∠ABC /2 = 60°/2 = 30° , следовательно
1. ΔADB равнобедренный AD = BD и
2. из ΔDBC: CD = BD /2 как катет против угла ∠CBD =30°
CD / AD = 1/2 ⇔ 1 +CD / AD = 1/2 +1 ⇔AC/AD =3/2 ⇒AD =(2/3)*AC
AD =2*15 см / 3 = 10 см
ответ : BD= AD = 10 см .
- - - - - - - - - -
2-ой
CD /AD = BC / BA ( теорема о биссектрисе )
CD /AD =1/2 BC = BA/2 (снова как катет против угла A =30°)
* * * * * * * рисунок во приложении * * * * * * *
ВК⊥РТ. ОК=R=х. ОВ=2х, ВК=3х.
Площадь круга по условию равна сумме двух секторов, площадь каждого из них равна π. S=πR²=3π; R²=3; R=√3 см. ВК=3√3
ΔРВК. ∠РВК=30°; пусть РК=х, тогда ВР=2х. 4х²-х²=(3√3)²; 3х²=27; х=3 см.
РК=3 см; РТ=2·3=6 см.
РТ - средняя линия ΔАВС, АС=2·6=12 см.
ответ 12 см.