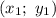есть координата первой точки на плоскости, а 
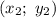– координата второй, тогда площадь прямоугольника, заключённого в этих точках, равна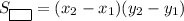 
ответ: 12 (ед. площади)
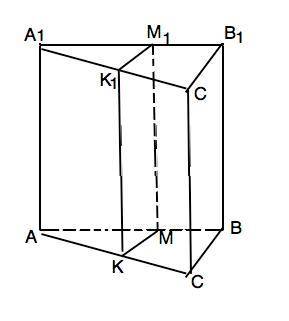
Объяснение: Площадь боковой поверхности призмы равна произведению высоты призмы на периметр основания: S=Н•Р=24
При проведении плоскости через среднюю линию основания параллельно боковому ребру плоскость сечения отсекает от оснований равные треугольники, подобные треугольникам оснований с коэффициентом подобия k=0,5а:а=1/2. Периметры подобных фигур относятся как их линейные размеры. Следовательно, S₂(бок)=Н•Р/2. Т.к. высота призмы не изменилась, S₂(бок)=24•1/2=12 (ед. площади)
