Если катеты 5 и 12 - гипотенуза 13. По теореме пифагора.
Центр описанной окружности будет лежать на середине гипотенузы.
Центр вписанной лежит на точке пересечения биссектрис.
Биссектриса делит противолежащую сторону в отношении прилежащих. Т.е. биссектриса из прямого угла разделит гипотенузу 5 к 12. Т.е. на 2 части... 65/17 и 156/17.
Ещё есть такая теорема
"Каждая биссектриса делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
Итак, находим длину биссектрисы.
Смотрим треугольник у которого один катет 5, второй - часть гипотенузы - 65/17. Мы знаем в нём косинус угла. (5/13) По теореме косинусов считаем.
l=5^2+(65/17)^2-5*(65/17)*cosA.
Итого l=sqrt(25-25/289).
Используем теорему, знаем, что она делится 17 к 13. Можем найти центр вписанной. Дальше мне уже лень считать)
Нужно вспомнить, что радиус описанной окружности вычесляется по формулe
r=(a*b*c)/(4*√p*((p-a)(p-b)(p-c))) эта формула большая большая
И долго считать
Ну вот тут у нас углы известным, причём все (углы у оснвоания по 60 выходит у и В угол 60)
Подойдет формула
r=a/(2*sin α) где а - сторона треугольника, а α - угол наротив этой стороны
вооот
возьмем за сторону а - известную сторону пять корень из трех
и альфа - это угол 60 градусов
синус 60 это корень из трех делить на два
r=(5√3)/(2*(√3/2))
дойка в знаменателе сокращается, и в общем знаменателе остается просто корень из трех
r=5√3/√3
радиус получается равень пяти
нужно было найти диаметр
диаметр, проще говоря, это два радиуса
значит диаметр равен 10
Решение для произвольного параллелограмма.
Пусть дан параллелограмм АВСD, ВС=AD - большие основания, т.О - середина АD, секущие прямые – ОМ и ОК.
Прямые не могут проходить через вершины В и С, иначе площади получившихся частей не будут равными.
Следовательно, прямые ОМ и ОК должны делить сторону ВС на 3 отрезка, а сам параллелограмм – на треугольник МОК и трапеции АВМО и ДСКО, средние линии которых для получения равновеликих фигур должны быть равны основанию МК треугольника (см. рисунок приложения).
Так как прямые проходят через середину большей стороны, средние линии трапеций равны (0,5•AD+BM):2=MK
Площадь каждой части равна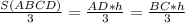
Формула площади треугольника S=h•а/2 ⇒
S ∆ MOK=h•MK:2=ВС•h/3 ⇒
2МК=ВС/3 ⇒ МК=2ВС/3
Примем ВМ=КС=m.
Тогда 2m=ВС-2ВС/3⇒
m=ВС/6
ОМ и ОК должны делить ВС в отношении 1:4:1
––––––––––––––––
Отмечаем середину оснований АD и ВС. Каждую половину ВС делим на 3 части и от В и С отмечаем М и К. ВМ=СК=ВС/6. Соединяем т.О на АD с т. М и К на ВС. Параллелограмм разделен на три равновеликие части.