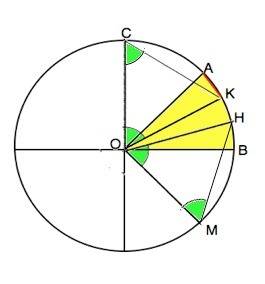
Дан угол АОВ=45°.
Из О как из центра чертим окружность произвольного радиуса. Проводим через О общепринятым перпендикулярно стороне ОВ прямую до пересечения с окружностью – диаметр.
Угол АОС=АОВ=45°.
Тем же радиусом из т. С делаем насечку в т. К на дуге АВ, т. К соединяем с т.О
Угол СОК=60° ( треугольник АОК - равносторонний)
Угол АОК=∠СОК-∠СОА=60°-45°=15°
а) Проводим биссектрису ОН угла КОВ. Данный угол поделен на 3 равные части. Или:
б) раствором циркуля, равным хорде АК. от т. В отмечаем на дуге АВ точку Н и соединим ее с О.
АОК=КОН=НОВ=15°.
-----------
Как вариант можно отложить от ОВ угол ВОМ=45° и от т.М тем радиусом ОВ отметить на дуге АВ т.Н.
ответ:Задание 1
Нам две внешний угол 150 градусов,сумма внешнего и внутреннего угла равна 180 градусов,поэтому мы можем узнать чему равен угол D
180-150=30 градусов
Так как треугольник АВD равнобедреный,то и угол А тоже равен 30 градусов,потому что в равнобедренном треугольнике углы при основании равны
Теперь найдём угол СВА
По условию треугольник АВС прямоугольный,угол АСВ=90 градусов
Сумма всех углов треугольника равна 180 градусов
180-(30+90)=60 градусов
Задание 2
Не понятно,что нужно узнать
Могу сказать,что треугольник равнобедреный
DB=BA
DC=AC
Сторона ВС-общая
Треугольники DBC и BCA равны между собой по третьему признаку равенства треугольников-если три стороны одного треугольника равны трём сторонам другого треугольника,то треугольники равны между собой
Есть в наличии внешний угол,он равен 60 градусов
Объяснение:
4. а)
5. а)
6. б)
7. а)
8. Да
9. г)
10. в)
Объяснение:
4. углы у равнобедренного треугольника при основании равны.
5. медиана - это своего рода биссектриса, а биссектриса делит угол пополам, следовательно, градусная мера угла АВС = 66 градусам.
6. если треугольник равнобедренный, то это не значит, что он равносторонний.
7. боковые стороны равностороннего треугольника равны, углы при основании тоже, следовательно равносторонний треугольник можно считать равнобедренным.
9. P=AB+BC+AC
AB=BC (как стороны равнобедренного треугольника)
AC= P-2AB
AC=7
10. P=AB+BC+AC
АВ=ВС=10
P= 26 (см)
∠АОВ=45°
Смотри фото. Если нужны объяснения спросишьПроводим окружность любого радиуса с центром в точке О.
Строим правильный вписанный 12 -х угольник, так как центральный угол в нем ∠ВОN=30° .
∠АОВ-∠ВОN=∠АОN=30°.
Проводим биссектрису ∠АОN. Получаем ∠NОР=∠АОР=15°.
∠АОВ поделен на три равные части.
Смотри фото. Если нужны объяснения спросишь
Поделить окружность на 12 равных частей очень даже просто:
1) строим окружность произвольного радиуса;
2) с двух перпендикулярных диаметров выделяем 4 точки на окружности (это концы диаметров);
3) Строим 4 вписанных правильных треугольника, вершины которых делят окружность на 12 равных дуг по 30° каждая. ∠АОN=30°. ∠ВОN=15°.
4) Строим биссектрису ∠АОN, которая поделит этот угол пополам по 15° каждый
∠ВОN=∠NОР=∠АОР=15°.