Объяснение:
№15
<ЕAD=180° развернутый угол.
<ВАС=<ЕAD-<BAE=180°-120°=60°
<BCA=90°, по условию.
Сумма острых углов в прямоугольном треугольнике равна 90°
<АВС=90°-<ВАС=90°-60°=30°
ответ: <ВСА=90°; <АВС=30°; ВАС=60°
№16
<АСD=180°, развернутый угол.
<ВСА=<АСD-<BCD=180°-120°=60°
∆ABC- равнобедренный треугольник АВ=ВС, по условию.
В равнобедренном треугольнике углы при основании равны.
<ВСА=<ВАС=60°
Сумма углов в треугольнике равна 180°
<АВС=180°-<ВСА-<ВАС=180°-60°-60°=60°
∆АВС- равносторонний.
ответ: так как треугольник равносторонний все углы имеют градусную меру 60°
Если 5,76 см², то и ответ будет в см: 2,4см
Объяснение:
Дано:
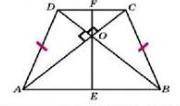
АВDC - трапеция
AD = BC
АС ⊥ DB
EF - средняя линия
Sтр. = 5,76см²
h - ? EF - ?
Высота трапеции — это перпендикуляр, проведенный из любой точки одного основания фигуры до другого.
Построим высоту ЕF⊥ АВ .
Sтр = (a + b)/2 * h, где a и b - основания трапеции.
Sтр = h* (АВ * DC)/2 = 5,76см²
1) Теорема: если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований, т.е.
h = (АВ * DC)/2, тогда
Sтр = h* (АВ * DC)/2 =h*h = h² = 5,76см², откуда
h = √5,76 = 2,4см
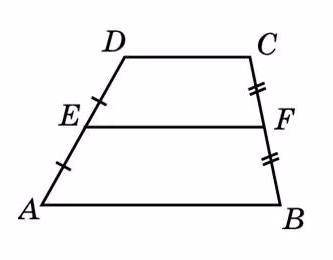
2) Средняя линия трапеции - отрезок, соединяющий середины боковых сторон и расположенный параллельно основаниям. Длина средней линии, равна полусумме оснований.
ЕF = (АВ * DC)/2 = h = 2,4 см (рис.2)
(На рис. 2 лучше измените буквы F и Е на другие, например, К и М.
Тогда средняя линия будет КМ = (АВ * DC)/2 = h = 2,4 см
А то получилось и выосота и ср. линия с одинаковыми буквами)
S=√(p(p-a)(p-b)(p-c))
p=(a+b+c)/2=(4+5+6)/2=7.5 см
S=√(7.5*3.5*2.5*1.5)=9.922 см²
S=ab*sinα/2
Найдём значение sinα между сторонами 4 и 6 см
sinα=2S/ab=2*9.22/4*6=0.826, α=55.77°
Проекция
4*cos(55.77°)=2.25 см
ответ проекция стороны длиной 4 на сторону длиной 6 равна 2.25 см
Второй решения задачи
По теореме косинусов имеем
5²=4²+6²-2*4*6*cosα
25-16-36=-12*4*cosα
4*cosα=27/12=2.25 см
ответ проекция стороны длиной 4 см на сторону длиной 6 см равна 2.25 см