Объяснение:
Обозначим наш треугольник точками АВС, в котором угол В = 120°, так как сторона АВ = ВС следовательно угол А = С (свойства равнобедренных треугольников), а поскольку сумма углов треугольника равна 180°, тогда сумма углов А и С равняется 180-120=60, то есть А = С = 30°.
Проводим высоту ВD, которая образует прямоугольный треугольник АВD. Катет ВD лежит против угла 30°, значит равен половине гипотинузы АВ. ВD = 6/2 = 3. По теореме Пифагора находим второй катет АD.
АD = √(36-9)=√27=3√3
Так как в равнобедренном треугольнике высота является и медианой, тогда АС = АD + DС = 3√3 + 3√3 = 6√3
Периметр треугольника - это сумма всех сторон
Р = 6√3 + 6 + 6 = 6√3 + 12
ответ: 6√3 + 12
П.С. я вроде бы все понятно расписал, надеюсь, что рисунок сделаешь сам(а), если нет пиши в комментарии я сфоткаю, отправлю
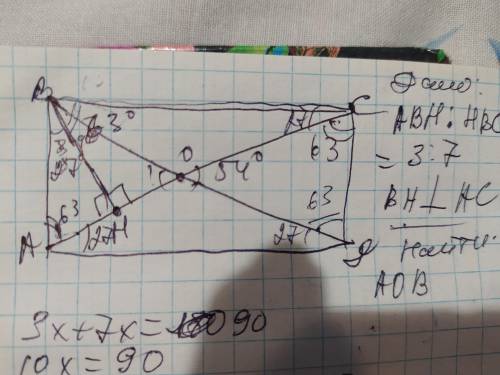
ответ: 54°
Объяснение: обозначим прямоугольник АВСД с диагональю АС и перпендикулярно ВН. Обозначим соотношение углов АВН и НВС как 3х и 7х. Зная, что они части прямого угла В, составим уравнение:
3х+7х=90
10х=90
х=90÷10
х=9
Теперь найдём части этих углов, зная х: угол АВН=3×9=27°;
Угол НВС=7×9=63°
Теперь рассмотрим полученный ∆АВН. Он прямоугольный и, зная угол ААН=27° и угол ВНА=90°, найдём угол ВАН: угол ВАН=180-27-90=63°. Рассмотрим ∆АОД. Так как в прямоугольнике диагонали, пересекаясь, делятся пополам, то этот треугольник равнобедренный: сторона АО=ОД и углы при основании равны: угол ОАД=углу ОДА. Так как угол А и угол Д полностью составляют 90°, то угол ОАД=углу ОДА=90-63=27°. Теперь найдём в этом треугольнике угол АОД: 180-27×2=180-54=126° Угол АОД=углуВОС=126°. Зная, что сумма углов в точке О составляет 360°, то сумма двух других острых углов будет составлять: 360-126×2= 360-252=108°
Так как эти углы равны, то искомый угол АОВ=углу СОД=108÷2=54°
Итак: угол АОВ=углу СОД=54°
Зададим сразу расстояние одной из прямых , пусть A1D1 , чтобы не вписывать множество переменных для произвольного шестиугольника , определим координаты 5 вершин произвольным образом , учитывая условно заданные расстояние и выпуклость , положим что
A(0,0) , B(3,0) , C(5,sqrt(12)) , D(3,7) , E(-2,8) , F(a,b)
При этом AB=3 , BC=4 , ED=5.
Тогда
A1(3/2,0)
B1(4, sqrt(3))
C1(4, 7/2+sqrt(3))
D1(1/2, 15/2)
E1((a-2)/2 , (b+8)/2)
F1(a/2, b/2)
Из условия A1D1=B1E1=F1C1 , получаем
(a-10)^2+(b+8-sqrt(12))^2=(a-8)^2+(b-7-sqrt(12))^2
откуда b=2a/15+(20*sqrt(3)-17)/10
Через скалярные произведение векторов найдём угол между векторами B1E1 и A1D1
cosa=(20-2a+15(b+8-sqrt(12)))/229
Подставляя найденный b и преобразовывая , получаем что cosa=1/2 или a=60 гр.
ответ 60 градусов .