Пункт В) тупоугольный треуголь
ник.
Объяснение:
В треугольнике выполняется
соотношение: против больше
го угла лежит большая сторо
на.
Сначала проверяю теорему
Пифагора. В прямоугоьном
треугольнике большей сто
роной является гипотенуза.
18^2=6^2+13^2
324=36+169
324>205
Так как условие теоремы не
выполняется, значит, треуголь
ник не прямоугольный. То есть
против большей стороны нахо
дится угол, превосходящий пря
мой. Чтобы убедиться, что треу
гольник тупоугольный, исполь
зуем теорему косинусов.
18^2=6^2+13^2-2×6×13cosa
156cosa=36+169-324
156cosa=-119
cosa=-119/156<0
cosa<0
Угол "а" - тупой.
Треугольник тупоугольный.
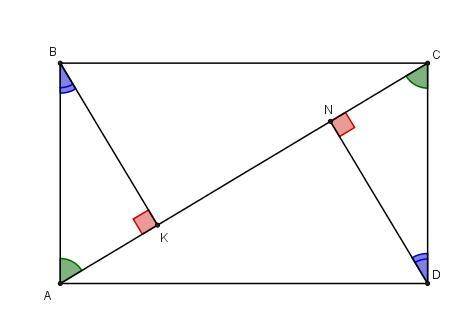
∠BAC = ∠ACD как накрест лежащие углы при AB || CD и секущей AC.
AB = CD, следовательно, ΔABK = ΔCND по гипотенузе и острому углу
У равных треугольников соответствующие элементы (стороны, углы) равны, т.е. BK = DN; CN = AK.
Рассмотрим прямоугольный треугольник BKC: по т. Пифагора
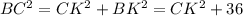 (*)
(*)
Рассмотрим прямоугольный треугольник ABC: по т. Пифагора
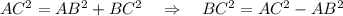
Подставляем теперь в равенство (*), получаем
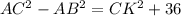
AB² найдем по теореме Пифагора из прямоугольного треугольника ABK, значит
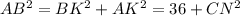
Все данные у нас есть, осталось решить уравнение
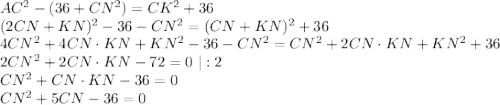
Получили квадратное уравнение, которое можно решить через дискриминант
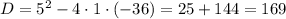
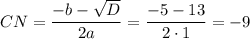 - не удовлетворяет условию
- не удовлетворяет условию
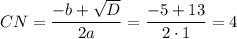 см
см
Следовательно, AC = 2*4 + 5 = 13 см, тогда
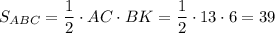 см²
см²
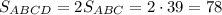 см²
см²
Второй решения:
У треугольников ABK и BKC прямые углы равны и ∠ABK = ∠BCK, следовательно, ΔABK ~ ΔBKC, из подобия треугольников следует, что BK/CK = AK/BK
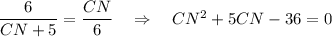
Такое же уравнение как в первом
ответ: 78 см².
Приравняем правые части уравнений, так как в точке пересечения ординаты (значения у) совпадают.
x² = 6 - x
x² + x - 6 = 0
D = 1 + 24 = 25 = 5²
x = (- 1 + 5)/2 = 2 или x = (-1 - 5)/2 = - 3
Абсциссы точек пересечения х = - 3 и х = 2.