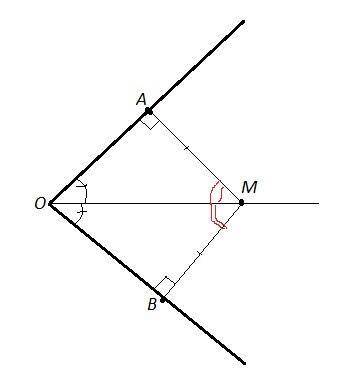
Расстояние от точки М (на биссектрисе) до стороны угла измеряется длиной перпендикуляра, опущенного из этой точки на сторону угла.
∠МАО=∠МВО=90°
∠АОМ=∠ВОМ, так как ОМ- биссектриса.
Соответственно
∠АМО=90°-∠АОМ
∠ВМО=90°-∠ВОМ- как острые углы прямоугольного треугольника
Можем утверждать, что ∠АМО=∠ВМО,
По второму признаку равенства треугольников: сторона и два прилежащие к не угла( ОМ- общая, ∠АМО=∠ВМО и ∠АОМ=∠ВОМ)
ΔАОМ=ΔВОМ. В равных треугольниках против соответственно равных углов лежат равные стороны, отсюда МА=МВ, что и требовалось доказать
2-ой угол = х + 30
3-ий угол = 2х
Сумма всех углов треугольника = 180°
Составим уравнение:
х + х + 30 + 2х = 180
4х = 180 - 30
4х = 150
х = 37,5
х + 30 = 37,5 + 30 = 67,5
2х = 37,5 * 2 = 75
ответ: 37,5° - один угол; 67,5° -другой угол; 75° - третий угол