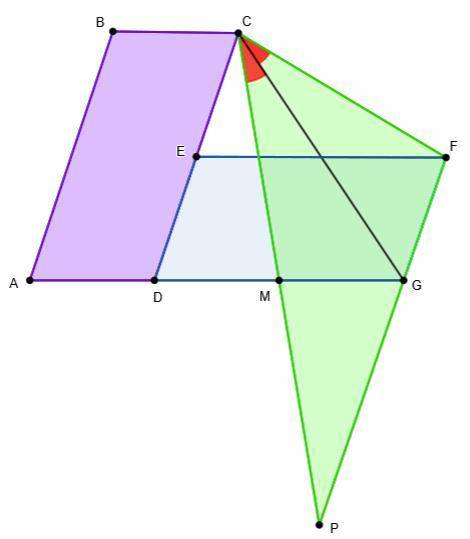
AB=CD - по свойству параллелограмма ABCD
AB=2*DE=CD ⇒ точка Е - середина CD
CE=ED=AD=DM=MG ⇒ CD=DG
четыр-ник ECFG - параллелограмм
CE || FG, так как ED || FG - по свойству параллелограмма EDGFCE=FG, так как ED=FG - по свойству параллелограмма EDGFЗначит, СF=EG - по свойству параллелограмма ECFG
ΔCDG - равнобедренный ⇒ CM=GE - медианы, проведенные к боковым сторонам равнобедренного треугольника
Поэтому CF=CM
Продолжим прямую СM до пересечения с прямой FG в точке P
ΔCMD=ΔPMG - по стороне и двум прилежащим к ней углам
DM=MG - по условию∠CMD=∠PMG - как вертикальные углы∠CDG=∠PGD - как накрест лежащие углы при CD || PG и секущей DGЗначит, CM=MP, CD=PG
Рассмотрим ΔСPF: CF=CM=MP, PG=2*FG
FG/PG=1/2 и CF/CP=1/2
Известное свойство биссектрисы:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам
Это свойство работает и в обратную сторону.
Следовательно, CG - биссектриса угла MCF, ч.т.д.
Уравнение окружности имеет вид:
(x-a)^2+(y-b)^2=r^2
в нашем случае
a=-3
b=2
r=sqrt(x1-x2)^2+(y1-y2)^2)
r=sqrt(0-(-3))^2+(-2-2)^2)=5
и уравнение имеет вид
(x+3)^2+(y-2)^2=25