Площадь равнобедренной трапеции равна полусумме оснований, умноженной на высоту.
Высота у нас уже есть Одно из оснований - тоже. Теперь надо найти большее основание. Если опустить высоту с меньшего основания на большее, то получим прямоугольный треугольник, где гипотенузой будет боковая сторона, одним из катетов - высота трапеции, а вторым катетом - часть основания трапеции. Чтобы узнать большее основание трапеции, нам нужно вычислить этот неизвестный катет в треугольнике, потому что длиной большего основания будет сумма двух таких катетов с меньшим основанием. Так как точно такой же треугольник можно получить, опустив высоту из другой точки меньшего основания трапеции. По теореме Пифагора вычисляем неизвестный катет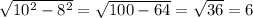 
. Значит длина наибольшего катета равна 7+6+6=19 см.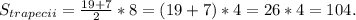 
ребро будет являться высотой.
Sбок=Pосн*H
Росн=Sбок/Н=240/10=24
у ромба все стороны равны, значит сторона равна P/4=24/4=6 см
диагонали в ромбе делят углы,из которых они выходят, пополам.
проведем диагонали и получим 4 равных треугольника.пересекаются диагонали между собой под прямым углом.
рассмотрим один из треугольников. у него один угол будет прямым(где диаг пересек), второй 30(угол ромба делится диагональю пополам), третий соответственно 60. в треугольнике с углом 30 гр катет, лежащий напротив этого угла, равен половине гипотенузы.гипотенуза равна стороне ромба, т.е 6, значит половина диагонали будет 3 (половина стороны).вся диагональ будет 6.
вторую диагональ можно найт практически таким же обраом,рассмотрев треугольник. по т.Пифагора найдем второй катет в прямоуг треуг катет в квадрате равен гипотенуза в квадр - второй катет в кв= 6*6-3*3=36-9=25
извлекая корень получим 5 - это половина диаг, вся диаг равна 10.
нам нужна меньшая, для рассчетов возьмем ее- 6 см.
в сечении будет прямоугольник.длина будет у него 6 см(диагональ), а ширина - ребро - 10 см
Sпрямоуг=a*b=10*6=60 см^2
3-я сторона х
х^2=49+64-2*7*8*(-0,5)=169
х=13
ответ 13