Формула радиуса окружности, описанной около правильного треугольника ⇒
Объяснение:
Центром описанной около треугольника окружности является точка пересечения его срединных перпендикуляров.
В проаильном треугольнике срединные перпендикуляры - высоты, биссектрисы, медианы.
Все стороны правльного треугольника равны, и все углы равны 60°.
Так как срединные перпендикуляры еще и медианы, точка пересечения делит их в отношении 2:1, считая от вершины. Все медианы правильного треугольника равны, а больший отрезок медианы - радиус описанной окружности.
Положим что прямая параллельная AC и проходящая через M , пересекает AB и AC в точках N и Y соотвественно , аналогично Z и X точки на BC и AC соотвественно , так же L , W на AC и BC . Так как прямые па аралелльны , то четырёхугольники LMXA , MNBZ , MWCY параллелограммы . Значит AL=XM , MY=WC , MX=BN . Полученные три треугольника подобны между собой , получаем (LN/MX)^2 = (27/12) (ZW/MY)^2 = (3/12) (MZ/LN)^2 = (3/27)
LN/MX=3/2 ZW/MY=1/2 MZ/LN=1/3
Откуда LN+AL = LN+MX = 5MX/2 Из подобия треугольников NML и ANY получаем (LN/(LN+AL))^2 = 27/(27+S(ALMX) + 12) Или 9/25 = 27/(39+S(ALMX)) Откуда S(ALMX) = 36 Аналогично и с двумя другими S(MNBZ)=18 , S(MYCW) = 12 Значит S(ABC) = 27+12+3+36+18+12 = 108
Формула радиуса окружности, описанной около правильного треугольника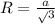 ⇒
⇒
Объяснение:
Центром описанной около треугольника окружности является точка пересечения его срединных перпендикуляров.
В проаильном треугольнике срединные перпендикуляры - высоты, биссектрисы, медианы.
Все стороны правльного треугольника равны, и все углы равны 60°.
Так как срединные перпендикуляры еще и медианы, точка пересечения делит их в отношении 2:1, считая от вершины. Все медианы правильного треугольника равны, а больший отрезок медианы - радиус описанной окружности.
ВВ1=АВ•sin60°
BB1=4√3•√3/2=6
R=BO=6:3•2=4 (ед. длины)