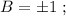
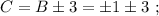
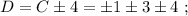
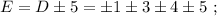
Пусть A - Начало координат
Ось X - AB
Ось Y - AD
Ось Z - перпендикулярно плоскости ABC в сторону S
Пусть O - центр квадрата ABCD
Найдем высоту пирамиды SABCD - SO
Из прямоугольного треугольника ABC
AC = 7√2
AO= 7√2 / 2
Из прямоугольного треугольника SOA
SA = 14
AO= 7√2 / 2
SO = √ ( SA^2-AO^2)= 7√14/2
Координаты точек
N ( 2;7;0)
K ( 3.5+ 2/7 * 3.5 ; 3.5+ 2/7 * 3.5 ; 5/7 * 7√14/2) K(4.5;4.5;2.5*√14)
Вектор
AS ( 3.5;3.5; 3.5*√14)
Мы знаем что плоскость a параллельна AS - Значит ей принадлежит точка L отложенная от K на вектор минус AS ( минус для удобства )
L(4.5- 3.5 ; 4.5 -3.5 ; 2.5*√14 - 3.5*√14) L( 1; 1; -√14)
N K L - определяют нашу плоскость.
Уравнение плоскости
ax+by+cz+d=0
Подставляем координаты точек N K L
2a+7b+d=0
4.5 a + 4.5 b + 2.5*√14 c + d=0
a + b - √14 c +d =0
Пусть d= -2 , Тогда b=0 a =1 c = -1/√14
Искомое уравнение
x - z/√14 -2 =0
a) Так как коэффициент при y =0 , а прямая BC параллельна оси Y , наша плоскость параллельна BC . Доказано
б )
Нормализованное уравнение плоскости
k= √(1+1/14) = √(15/14)
x/k - z/k/√14 -2/k =0
Подставляем координаты точки B ( 7;0;0) в нормализованное уравнение для определения искомого расстояния
7/√(15/14) - 2 / √(15/14) = 5 / √(15/14) = √210 / 3
(x₁; y₁) и (x₂; y₂)
r = √((x₂-x₁)² + (y₂-y₁)²) (*)
Расстояние между точками равно радиусу окружности. Подставляем в формулу (*) координаты наших двух точек
r = √((1-(-2))²+(-3-5)²)= √(3²+8²) = √(9+64) = √73
Уравнение окружности с центром в точке (x₀; y₀) радиусом r
(x - x₀)² + (y - y₀)² = r²
И уравнение окружности с центром в точке (1; -3) и радиусом √73
(x-1)² + (y+3)² = 73