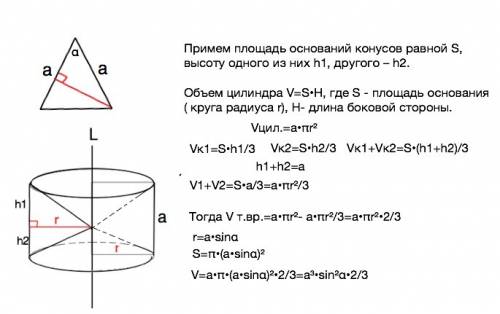
Тело, которое получится вращением равнобедренного треугольника вокруг оси, проходящей через вершину основания параллельно боковой стороне, - цилиндр, из которого "вырезаны" конусы с основаниями, равными основаниям цилиндра, и общей вершиной.
Радиусом r оснований такого тела будет высота данного треугольника, проведенная к его боковой стороне.
Примем площадь оснований цилиндра и конусов равной S, высоту одного из них h1, другого – h2.
Объем цилиндра Vцил.=S•H, где S - площадь основания ( круга радиуса r), Н- длина боковой стороны стороны треугольника.
Vцил.=а•πr²
Обозначим объемы конусов V1 и V2, тогда
V1=S•h1/3
V2=S•h2/3 сумма их объёмов V1+V2=S•(h1+h2)/3
h1+h2=a
V1+V2=S•a/3=a•πr²/3
Тогда V=Vцил-(V1+V2)
V=а•πr² - а•πr²/3=а•πr²•2/3
r=a•sinα S=π•(a•sinα)²
V=а•π•(a•sinα)²•2/3=a³•sin²α•2/3