Если точка C(x0, y0) делит отрезок с концами в точках A(x1, y1) и B(x2, y2) в отношении 2 : 3, считая от точки A, то по теореме о пропорциональных отрезках проекция точки C на ось OX делит проекцию отрезка AB на эту ось в том же отношении, то есть = ⅔. Отсюда находим, что
x0 = ⅕ (3x1 + 2x2) = (3·(–6) + 2·4) : 5 = –2.
Аналогично y0 = ⅕ (3y1 + 2y2) = (3·1 + 2·6) : 5 = 3.
ответ
(–2, 3).
Источники и прецеденты использования
web-сайт
Название Система задач по геометрии Р.К.Гордина
URL http://zadachi.mccme.ru
задача
Номер 4235
∠АВН = 30°; ∠ВАР = 45°.
Пошаговое объяснение:
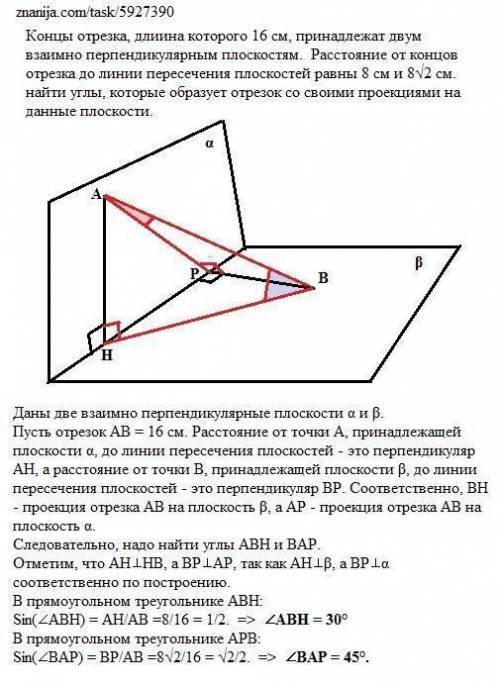
Концы отрезка, длина которого 16 см, принадлежат двум взаимно перпендикулярным плоскостям. Расстояние от концов отрезка до линии пересечения плоскостей равны 8 см и 8√2 см. найти углы, которые образует отрезок со своими проекциями на данные плоскости.
Решение.
Даны две взаимно перпендикулярные плоскости α и β.
Пусть отрезок АВ = 16 см. Расстояние от точки А, принадлежащей плоскости α, до линии пересечения плоскостей - это перпендикуляр АН, а расстояние от точки В, принадлежащей плоскости β, до линии пересечения плоскостей - это перпендикуляр ВР. Соответственно, ВН - проекция отрезка АВ на плоскость β, а АР - проекция отрезка АВ на плоскость α.
Следовательно, надо найти углы АВН и ВАР.
Отметим, что АН⊥НВ, а ВР⊥АР, так как АН⊥β, а ВР⊥α соответственно по построению.
В прямоугольном треугольнике АВН:
Sin(∠АВН) = АН/АВ =8/16 = 1/2. => ∠АВН = 30°
В прямоугольном треугольнике АРВ:
Sin(∠ВАР) = ВР/АВ =8√2/16 = √2/2. => ∠ВАР = 45°.
найдем объем 0,604/8900
объем цилиндра равен h*Пd^2/4
d^2=4V/(h*П)=4*0,604/(8900*150*П)
d~7,6*10^(-3)*C (м)