ответ: Объем шарового сегмента опущенного в цилиндр = π*468 см³
Объяснение: Дано:
Диаметр шара = 30 см тогда его радиус R = 15
Радиус основания цилиндра r = 12см
Найти объем шарового сегмента, опушенного в цилиндр V - ?
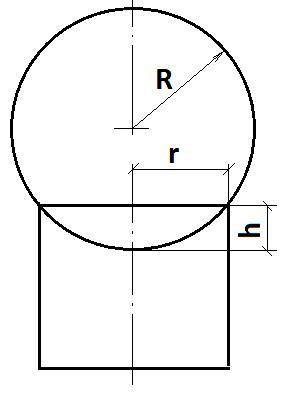
Смотрите рисунок. Что бы найти объем надо найти размер h - глубину погружения шара. По теореме Пифагора R² = r² + (R-h)² Получили квадратное уравнение: h² - 2Rh + r² = 0
h1,2 = (2R+-√4R² - 4r²)/2 = (2R+-2√R²-r²)/2 h = 6 см
Объем шарового сегмента найдем по формуле V = π*h²(R - h/3) = π*468 см³
1. Первоначальные сведения по геометрии появились за 4-5 тысячелетий до наших дней в Древнем Египте. В этих краях ежегодные разливы Нила смывали посевы. Поэтому для того чтобы восстанавливать посевы и уточнять размеры налогов, необходимо было размечать поля и выполнять необходимые подсчёты.
2. Древнегреческие учёные переняли у египтян измерения и учёта земель и назвали эти знания геометрией. "Геометрия" - слово, происходящее от греческих слов "reo" - земля, "метрео" - измерять.
3. Евклид, Пифагор, Мухаммад аль-Хорезми, Ахмад Фергани, Абу Райхан Беруни, Абу Али ибн Сина.
4. Памятник Кок Минор напоминает нам форму цилиндра, а на его поверхности фигуры, похожие на круги, овалы и ромбы.
5. Геометрия изучает пространственные структуры и отношения.
Объяснение:
Вроде всё!)
Значит, сумма 2 неизвестных углов = 180 - 18 = 162°.
Чтобы найти угол между биссектрисами двух "других" углов, следует рассматривать этот угол (назовём его угол С), как один из углов треугольника, образуемого двумя пересекающимися биссектрисами.
Т.к. биссектриса делит угол на 2 равные части, то сумма углов, в образуемом треугольнике = 162÷4×2 = 40,5×2 = 81°.
Тогда, сумма нужного нам угла С будет равна = 180 - 81 = 99°
ответ: угол, образуемый между биссектрисами двух других углов = 99°