Объяснение:
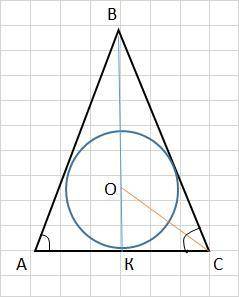
ΔАВС - равнобедренный, АВ = ВС
АС - основание, h = ВК - высота Δ- ка
О - центр вписанной окружности
(Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. Поскольку в равнобедренном треугольнике биссектриса, проведенная к основанию, совпадает с медианой и высотой, то центр вписанной в равнобедренный треугольник окружности лежит на высоте и медиане, проведенных к основанию).
Соединим т.О и т.С.
Т.к. ВК⊥ АС, то ΔОКС - прямоугольный.
ОС - биссектриса, поэтому ∠ОСК = 30°/2 = 15°
r /КС = tg 15° → r = KC * tg 15°
h = tg30°* KC
h - r = 2 по условию, поэтому
KC*tg30° - KC * tg 15° = 2
КС(tg30°- tg 15°) = 2
КС = 2 / (tg30°- tg 15°)
АС = 2КС = 4 / (tg30°- tg 15°)
Объяснение:
№15
<ЕAD=180° развернутый угол.
<ВАС=<ЕAD-<BAE=180°-120°=60°
<BCA=90°, по условию.
Сумма острых углов в прямоугольном треугольнике равна 90°
<АВС=90°-<ВАС=90°-60°=30°
ответ: <ВСА=90°; <АВС=30°; ВАС=60°
№16
<АСD=180°, развернутый угол.
<ВСА=<АСD-<BCD=180°-120°=60°
∆ABC- равнобедренный треугольник АВ=ВС, по условию.
В равнобедренном треугольнике углы при основании равны.
<ВСА=<ВАС=60°
Сумма углов в треугольнике равна 180°
<АВС=180°-<ВСА-<ВАС=180°-60°-60°=60°
∆АВС- равносторонний.
ответ: так как треугольник равносторонний все углы имеют градусную меру 60°
Из данных ,что боковая сторона и диагональ основания взаимно перпендикулярны и равны соответственно 15 см и 20 см, то большее основание трапеции равно 25 см (по Пифагору).
Находим косинус угла Д.
cos Д = (15² + 25² - 20²)/(2*15*25) = 0,6.
Синус Д = √(1 - 0,6²) = 0,8.
Находим сторону ВС:
ВС = АД - 2*СД*cos Д = 25 - 2*15*0,6 = 25 - 18 = 7 см.
Средняя линия трапеции в основании призмы и сечения равна:
Lср = (25 + 7)/2 = 32/2 = 16 см.
Наклонная высота hc сечения равна: 320/16 = 20 см.
Высота трапеции h в основании призмы равна 15*sin Д = 15*0,8 = 12 см.
Тогда высота призмы H равна:
H =√(20² - 12²) = √(400 - 144) = √256 = 16 см.
Определяем объём призмы:
V = So*H = Lср*h*H = 16*12*16 = 3072 см³.