Объяснение:
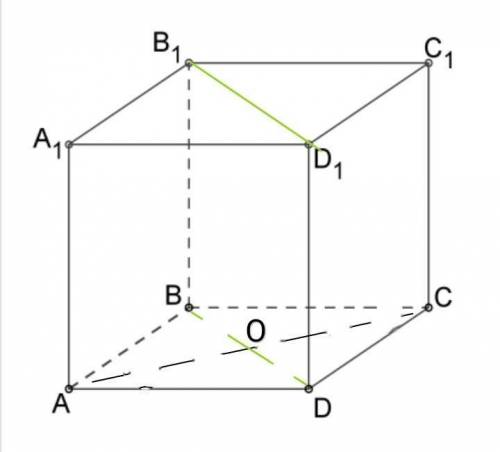
1) Все грани куба являются квадратами.
По свойствам квадрата диагонали взаимно перпендикулярны. В нашем случае АС ⟂ BD.
2) DD1 ⟂ DC по условию и DD1 ⟂ DA, DC ⋂ DA = D, тогда по признаку перпендикулярности прямой и плоскости DD1 ⟂ (ABC).
3) Так как DD1 ⟂ (ABC) , то она перпендикулярна любой прямой, лежащей в этой плоскости, в том числе DD1 ⟂ AC.
4) Получили, что
АС ⟂ BD, AC ⟂ DD1, BD ⋂ DD1 = D, тогда по признаку перпендикулярности прямой и плоскости АС ⟂ (ВВ1D1), что и требовалось доказать.
1.Преобразования плоскости
Преобразованием плоскости называют правило, с которого каждой точке плоскости ставится в соответствие точка этой же плоскости. ... Точку F(M) называют образом точки M при преобразовании F, а точку M называют прообразом точки F(M) при преобразовании F.
2.Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной точки О, называется преобразованием симметрии относительно точки О. При этом фигуры F и F' называются симметричными относительно точки О.
4.Другое определение: фигура центрально-симметрична, если для каждой точки фигуры точка, симметричная ей относительно центра симметрии, тоже принадлежит фигуре. Примеры центрально-симметричных фигур: окружность, параллелограмм, правильная шестиконечная звезда.
5.Центра́льной симметри́ей относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через, в то время как обозначение можно перепутать с осевой симметрией.
3.

1.
М - середина АВ, значит МВ = АВ/2
Р - середина МВ, значит РВ = МВ/2 = АВ/4
К - середина ВС, значит КС = ВС/2
Е - середина КС, значит ЕС = КС/2 = ВС/4
N - середина АС, значит NA = АС/2
G - середина NA, значит GA = NA/2 = AC/4
По условию
PB + EC + GA = 12
АВ/4 + ВС/4 + АС/4 = 12
1/4 · (АВ + ВС + АС) = 12
АВ + ВС + АС = 12 · 4 = 48 (см)
2.
Из решения первой задачи следует, что
АР = 3/4 АВ
ВЕ = 3/4 ВС
CG = 3/4 AC
По условию
AP + BE + CG = 108
3/4 АВ + 3/4 ВС + 3/4 АС = 108
3/4 · (АВ + ВС + АС) = 108
АВ + ВС + АС = 108 · 4/3 = 144 (см)