ответ: Такого треугольника не может быть.
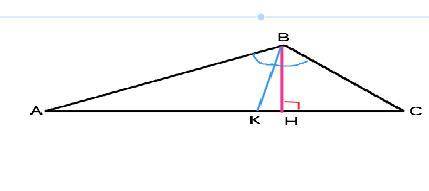
Объяснение: Биссектриса делит угол 130° на 2 равных по 65°.
Высота отсекает от треугольника прямоугольный треугольник с острым углом между высотой и боковой стороной 15°. (65°-50°=15°). Сумма острых углов треугольника 90°. Поэтому второй острый угол этого треугольника будет 90°-15°=75°. Получится, что сумма двух углов треугольника 130°+75°=205°, чего быть не может. А есть ведь ещё и третий угол.
Встречается подобная задача, где угол между высотой и биссектрисой 10°. Тогда решение возможно. Углы при основании получим 35° и 15°. При проверке сумма углов треугольника 130°+35°+15°=180°.
Подробное решение такой задачи дано мной на
Пусть m - прямая, проходящая через точку А, и k - прямая, проходящая через точку В.
Через две параллельные прямые проходит единственная плоскость.
По условию k║m, значит эти прямые лежат в одной плоскости α.
А∈m, m∈α, ⇒ A∈α
B∈k, k∈α, ⇒ B∈α.
Пусть М - точка пересечения прямых m и а, К - точка пересечения прямых k и а.
Тогда точки К и М также лежат в плоскости α.
По аксиоме: если две точки прямой лежат в плоскости, то и все точки прямой лежат в этой плоскости,
значит а∈α.
Итак, точки А, В и прямая а лежат в одной плоскости.